题目内容
如果直线a?β，直线b?β，l∩α=A，l∩β=A．试判断直线l与平面β的关系并说明理由．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：利用空间线线、线面、面面间的位置关系求解．
解答：
解：∵直线a?β，直线b?β，l∩α=A，l∩β=A，
∴平面α与β相交，
设α∩β=m，点A∈m，且l∩m=A，
∴直线l∩平面β=A．
∴直线l与平面β相交．
∴平面α与β相交，
设α∩β=m，点A∈m，且l∩m=A，
∴直线l∩平面β=A．
∴直线l与平面β相交．
点评：本题考查直线与平面的位置关系的判断，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
已知-1和2是函数y=x2+bx+c的两个零点，则不等式bx2+bx-c＜0的解集为（ ）
| A、（-1，2） |
| B、（-2，1） |
| C、（-∞，-1）∪（2，+∞） |
| D、（2，+∞） |
已知变量x、y满足条件
，则2x+y的最大值是（ ）
|
| A、3 | B、6 | C、9 | D、12 |
若实数x，y满足不等式组
且x+y的最大值为6，则实数m=（ ）
|
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
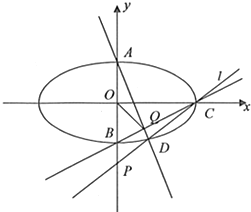如图，已知连接椭圆