题目内容
已知函数f(x)=
ax2+lnx(a∈R)
(1)若曲线y=f(x)在x=1处的切线与直线x-y=0垂直,试分析方程f(x)=0的解的个数;
(2)若函数f(x)在[1,2]上单调递增,求实数a的取值范围;
(3)若x>1,求证:4-8ln2+8ln(1+
)<(1+
)2<8ln(1+
)+1.
| 1 |
| 2 |
(1)若曲线y=f(x)在x=1处的切线与直线x-y=0垂直,试分析方程f(x)=0的解的个数;
(2)若函数f(x)在[1,2]上单调递增,求实数a的取值范围;
(3)若x>1,求证:4-8ln2+8ln(1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
考点:利用导数求闭区间上函数的最值,函数的单调性与导数的关系,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由导数的几何意义k=f′(1)计算出a,再利用数形结合解题.
(2)由函数f(x)在[1,2]上单调递增转化为:f′(x)≥0在x∈[1,2]上恒成立,再由参数分离得到a≥-
,x∈[1,2],再进一步求解.
(3)
(2)由函数f(x)在[1,2]上单调递增转化为:f′(x)≥0在x∈[1,2]上恒成立,再由参数分离得到a≥-
| 1 |
| x2 |
(3)
解答:
解:(1)∵f(x)=
ax2+lnx(x∈R),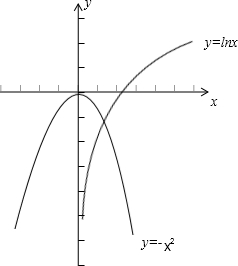
∴f′(x)=ax+
,x>0,
∴f′ (1)=a+1,
∵曲线y=f(x)在x=1处的切线与直线x-y=0垂直,
∴a+1=-1,解得a=-2.
∴f(x)=-x2+lnx,
在同一坐标系中,分别作出y=-x2和y=lnx的图象,
由图象知f(x)=-x2+lnx=0的解的个数只有1个.
(2)由函数f(x)在[1,2]上单调递增,知f′(x)≥0在x∈[1,2]上恒成立,
f′(x)=ax+
=
≥0,分离参数得,
a≥-
在x∈[1,2]上恒成立,
只须a≥(-
)max即可,
又-
在[1,2]上单调递増,∴(-
)max=-
,
∴a≥-
∴实数a的取值范围是[-
,+∞).
(3)∵x>1,∴0<
<1,∴1<1+
<2,
令a=-
,f(x)=-
x2+lnx,由(2)可知,f(x)在[1,2]上单调递增,
f(1)<f(1+
)<f(2),-
<-
(1+
)2+ln(1+
)<-
+ln2,化简得,
4-8ln2+8ln(1+
)<(1+
)2<8ln(1+
)+1.
| 1 |
| 2 |

∴f′(x)=ax+
| 1 |
| x |
∴f′ (1)=a+1,
∵曲线y=f(x)在x=1处的切线与直线x-y=0垂直,
∴a+1=-1,解得a=-2.
∴f(x)=-x2+lnx,
在同一坐标系中,分别作出y=-x2和y=lnx的图象,
由图象知f(x)=-x2+lnx=0的解的个数只有1个.
(2)由函数f(x)在[1,2]上单调递增,知f′(x)≥0在x∈[1,2]上恒成立,
f′(x)=ax+
| 1 |
| x |
| ax2+1 |
| x |
a≥-
| 1 |
| x2 |
只须a≥(-
| 1 |
| x2 |
又-
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| 4 |
∴a≥-
| 1 |
| 4 |
∴实数a的取值范围是[-
| 1 |
| 4 |
(3)∵x>1,∴0<
| 1 |
| x |
| 1 |
| x |
令a=-
| 1 |
| 4 |
| 1 |
| 8 |
f(1)<f(1+
| 1 |
| x |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
4-8ln2+8ln(1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
点评:导数是高考中常考的知识点,在选择题,填空题以及解答题都有出现,本题中采用的也是经常考查的知识点和方法,其中参数分离在使用时是相对比较方便的,在第三问的处理中,直接利用第二问的结论化简即可,很多学生可能被冗长的题目吓到,其实,只要静下心来仔细分析,这些都是“纸老虎”,不难攻破.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
下列算式正确的是( )
| A、lg8+lg2=lg10 |
| B、lg8+lg2=lg6 |
| C、lg8+lg2=lg16 |
| D、lg8+lg2=lg4 |
若实数x,y满足不等式组
且x+y的最大值为6,则实数m=( )
|
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|