题目内容
如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于D，过点C作BD的平行线与圆交于点E，与AB相交于点F，AF=6，FB=2，EF=3，则线段CD的长为考点：与圆有关的比例线段
专题：直线与圆
分析：根据题设条件由相交弦定理求出FC=4，再由BD∥CE，求出BD=
，由切割线定理得BD2=CD•AD，由此能求出结果．
| 16 |
| 3 |
解答：
解：∵AF=6，FB=2，EF=3，
由相交弦定理得AF•FB=EF•FC，∴FC=4，
又∵BD∥CE，∴
=
，
∴BD=
•FC=
•4=
，
设CD=x，AD=4x，
由切割线定理得BD2=CD•AD，
即x•4x=（
）2，
解得x=
，∴CD=
．
故答案为：
．
由相交弦定理得AF•FB=EF•FC，∴FC=4，
又∵BD∥CE，∴
| AF |
| AB |
| FC |
| BD |
∴BD=
| AB |
| AF |
| 8 |
| 6 |
| 16 |
| 3 |
设CD=x，AD=4x，
由切割线定理得BD2=CD•AD，
即x•4x=（
| 16 |
| 3 |
解得x=
| 8 |
| 3 |
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本试题主要考查了平面几何中直线与圆的位置关系，相交弦定理，切割线定理，相似三角形的概念、判定与性质．
练习册系列答案
相关题目
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |
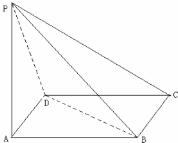四棱锥P-ABCD中，底面ABCD是边长为2a的菱形，∠BAD=60°，侧棱PA⊥平面ABCD，且PA=
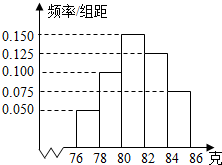某厂对一批产品进行抽样检测，图2是抽检产品净重（单位：克）数据的频率分布直方图，样本数据分组为[76，78）、[78，80）、…、[84，86]．若这批产品有120个，估计其中净重大于或等于78克且小于84克的产品的个数是