题目内容
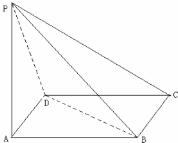四棱锥P-ABCD中，底面ABCD是边长为2a的菱形，∠BAD=60°，侧棱PA⊥平面ABCD，且PA=| 3 |
（1）二面角P-BD-A的大小；
（2）点A到平面PBD的距离．
考点：与二面角有关的立体几何综合题,点、线、面间的距离计算
专题：空间位置关系与距离
分析：（1）取BD中点M，由题设条件推导出∠PMA为二面角P-BD-A的平面角，由此能求出二面角P-BD-A的大小．
（2）设A到平面PBD的距离为h，由VA-PBD=VP-ABD，用等积法能求出A到平面PBD的距离．
（2）设A到平面PBD的距离为h，由VA-PBD=VP-ABD，用等积法能求出A到平面PBD的距离．
解答：
（1）解：如图，取BD中点M，
∵M为菱形中心，∴AM⊥BD，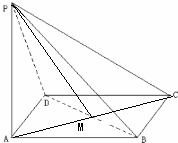
又∵PA⊥面ABCD，∴由三垂线定理，得PM⊥BD，
∴∠PMA为二面角P-BD-A的平面角．
∵ABCD是边长为2a的菱形，∴AB=AD，
又∵∠BAD=60°，∴△ABD为等边三角形，
∴AM=2acos30°=
a．
又∵△PAM为直角三角形，PA=
a，所以tan∠PMA=
=1，
∴二面角P-BD-A的大小为45°．
（2）解：设A到平面PBD的距离为h，
∵VA-PBD=VP-ABD，
∴S△ABD•PA•
=S△PBD•h•
，
S△ABD=
BD•AM=
a2，PA=
a，
∵AB=AD，PA⊥平面ABCD，∴PB=PD．
在△PBD中，DM=a，PD=
=
a，
∴PM=
a，∴S△PBD=
BD•PM=
a2．
∴
a2•2a=
a2•h，
解得h=
a．
∴A到平面PBD的距离为
a．
∵M为菱形中心，∴AM⊥BD，
又∵PA⊥面ABCD，∴由三垂线定理，得PM⊥BD，
∴∠PMA为二面角P-BD-A的平面角．
∵ABCD是边长为2a的菱形，∴AB=AD，
又∵∠BAD=60°，∴△ABD为等边三角形，
∴AM=2acos30°=
| 3 |
又∵△PAM为直角三角形，PA=
| 3 |
| PA |
| AM |
∴二面角P-BD-A的大小为45°．
（2）解：设A到平面PBD的距离为h，
∵VA-PBD=VP-ABD，
∴S△ABD•PA•
| 1 |
| 3 |
| 1 |
| 3 |
S△ABD=
| 1 |
| 2 |
| 3 |
| 3 |
∵AB=AD，PA⊥平面ABCD，∴PB=PD．
在△PBD中，DM=a，PD=
| PA2+AD2 |
| 7 |
∴PM=
| 6 |
| 1 |
| 2 |
| 6 |
∴
| 3 |
| 6 |
解得h=
| 2 |
∴A到平面PBD的距离为
| 2 |
点评：本题考查二面角大小的求法，考查点到平面的距离的求法，解题时要注意空间思维能力的培养，注意等积法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于D，过点C作BD的平行线与圆交于点E，与AB相交于点F，AF=6，FB=2，EF=3，则线段CD的长为