题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,b=2c,且B-C=
.
(1)求角C;
(2)若c=1,求△ABC的面积.
| π |
| 3 |
(1)求角C;
(2)若c=1,求△ABC的面积.
考点:正弦定理
专题:三角函数的图像与性质
分析:(1)将b=2c利用正弦定理化简,把B=
+C代入,利用两角和与差的正弦函数公式化简,整理后利用同角三角函数间的基本关系求出tanC的值,即可确定出C的度数;
(2)由C的度数求出B的度数为
,在直角三角形中,求出b与a的值,利用三角形面积公式即可求出△ABC的面积.
| π |
| 3 |
(2)由C的度数求出B的度数为
| π |
| 2 |
解答:
解:(1)∵b=2c,由正弦定理,得b=2RsinB,c=2RsinC,
∴将其代入,得sinB=2sinC,
∵B-C=
,∴B=
+C,
将其代入上式,得sin(
+C)=2sinC,
∴sin
cosC+cos
sinC=
cosC+
sinC=2sinC,即
cosC=
sinC,
整理得,
sinC=cosC,即tanC=
,
∵角C是三角形的内角,
∴C=
;
(2)∵C=
,∴B=
+
=
,
又∵c=1,∴b=2c=2,
∴根据勾股定理得:a=
=
,
∴S△ABC=
acsinB=
.
∴将其代入,得sinB=2sinC,
∵B-C=
| π |
| 3 |
| π |
| 3 |
将其代入上式,得sin(
| π |
| 3 |
∴sin
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
整理得,
| 3 |
| ||
| 3 |
∵角C是三角形的内角,
∴C=
| π |
| 6 |
(2)∵C=
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
又∵c=1,∴b=2c=2,
∴根据勾股定理得:a=
| b2-c2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
点评:此题考查了正弦定理,三角形的面积公式,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为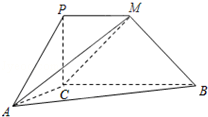 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.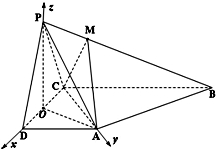 如图,在四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4.
如图,在四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4. 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.