题目内容
已知函数f（x）=
，下列命题：
①函数f（x）的零点为1；
②函数f（x）的图象关于原点对称；
③函数f（x）在其定义域内是减函数；
④函数f（x）的值域为（-∞，-1）∪（1，+∞）．
其中所有正确的命题的序号是 ．
| ex+e-x |
| ex-e-x |
①函数f（x）的零点为1；
②函数f（x）的图象关于原点对称；
③函数f（x）在其定义域内是减函数；
④函数f（x）的值域为（-∞，-1）∪（1，+∞）．
其中所有正确的命题的序号是
考点：命题的真假判断与应用,函数奇偶性的判断
专题：函数的性质及应用
分析：已知函数f（x）=
，
①由于ex＞0，e-x＞0，可得函数f（x）的无零点；
②由于函数的定义域为{x|x∈R且x≠0}，f（-x）=
=-f（x），因此函数f（x）是奇函数，即可得出图象的对称性；
③函数f（x）=
=1+
，当x＞0时，利用函数y=e2x单调递增，可得e2x＞1，函数f（x）在x＞0时单调递减；同理函数f（x）在x＜0时单调性质．但是在其定义域内不是单调函数；
④变形函数f（x）=1+
，当x＞0时，利用函数f（x）在x＞0时单调递减，可得f（x）＞1；利用奇函数的性质可得：当x＜0时，可得f（x）＜-1．即可得出函数f（x）的值域．
| ex+e-x |
| ex-e-x |
①由于ex＞0，e-x＞0，可得函数f（x）的无零点；
②由于函数的定义域为{x|x∈R且x≠0}，f（-x）=
| e-x+ex |
| e-x-ex |
③函数f（x）=
| e2x+1 |
| e2x-1 |
| 2 |
| e2x-1 |
④变形函数f（x）=1+
| 2 |
| e2x-1 |
解答：
解：已知函数f（x）=
，
①∵ex＞0，e-x＞0，∴函数f（x）的无零点，不正确；
②∵函数的定义域为{x|x∈R且x≠0}，f（-x）=
=-f（x），∴函数f（x）是奇函数，因此其函数f（x）的图象关于原点对称，正确；
③函数f（x）=
=1+
，当x＞0时，函数y=e2x单调递增，且e2x＞1，∴函数f（x）在x＞0时单调递减；同理函数f（x）在x＜0时单调递减，但是函数f（x）在其定义域内不是单调函数；
④函数f（x）=
=1+
，当x＞0时，函数f（x）在x＞0时单调递减，可得f（x）＞1；同理利用奇函数的性质可得：当x＜0时，可得f（x）＜-1．因此函数f（x）的值域为（-∞，-1）∪（1，+∞）．
综上可得：正确的命题为②④．
故答案为：②④．
| ex+e-x |
| ex-e-x |
①∵ex＞0，e-x＞0，∴函数f（x）的无零点，不正确；
②∵函数的定义域为{x|x∈R且x≠0}，f（-x）=
| e-x+ex |
| e-x-ex |
③函数f（x）=
| e2x+1 |
| e2x-1 |
| 2 |
| e2x-1 |
④函数f（x）=
| e2x+1 |
| e2x-1 |
| 2 |
| e2x-1 |
综上可得：正确的命题为②④．
故答案为：②④．
点评：本题考查了函数f（x）=
的单调性奇偶性值域及其零点，考查了推理能力与计算能力，属于中档题．
| ex+e-x |
| ex-e-x |
练习册系列答案
相关题目
已知直线y=-x+1与椭圆
+
=1（a＞b＞0）相交于A、B两点，若椭圆的离心率为
，焦距为2，则线段AB的长是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
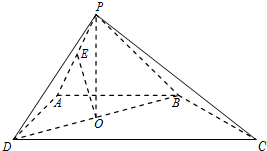如图，四棱锥P-ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．