题目内容
设集合A={x|x2-3x＜0}，集合B={y|y=2x，0≤x≤1}，则A∩B=（ ）
| A、（0，1] |
| B、（0，2] |
| C、[1，2] |
| D、[1，3） |
考点：交集及其运算
专题：集合
分析：分别解出集合A，B，然后求其A∩B即可．
解答：
解：A={x|x2-3x＜0}=（0，3），
集合B={y|y=2x，0≤x≤1}=[1，2]，
则A∩B=[1，2]，
故选C．
集合B={y|y=2x，0≤x≤1}=[1，2]，
则A∩B=[1，2]，
故选C．
点评：本题主要考查集合的基本运算，利用不等式求出对应的集合是解决本题的关键，比较基础．
练习册系列答案
相关题目
“a≥0”是“函数f（x）=|x+a|在区间（0，+∞）内单调递增”的（ ）
| A、充分而不必要条件 |
| B、充分必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
向量
=（1，2），
=（-2，k），若
与
共线，则|3
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、2
| ||
C、5
| ||
| D、5 |
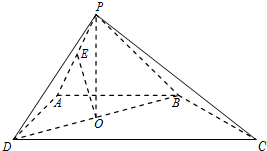如图，四棱锥P-ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．