题目内容
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,点M(0,2)关于直线y=-x的对称点在椭圆C上,且△MF1F2为正三角形,求椭圆C的方程.分析 由题意画出图形,求出M点关于直线y=-x的对称点,则a可求,再由△MF1F2为正三角形列式求得c,结合隐含条件求得b,则椭圆方程可求.
解答 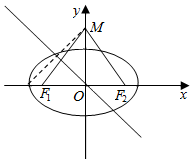 解:如图,
解:如图,
点M(0,2)关于直线y=-x的对称点为(-2,0),
∵(-2,0)在椭圆上,∴a=2,
又△MF1F2为正三角形,
∴tan30°=$\frac{c}{2}$,得c=2tan30°=2×$\frac{\sqrt{3}}{3}$,
则b2=a2-c2=4-$\frac{4}{3}=\frac{8}{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{8}$=1.
点评 本题考查椭圆的简单性质,考查了椭圆方程的求法,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.已知命题p:若x∈N*,则x∈Z.命题q:?x0∈R,${(\frac{1}{2})^{x_0}}=0$.则下列命题为真命题的是( )
| A. | ¬p | B. | p∧q | C. | ¬p∨q | D. | ¬p∨¬q |
12.下列方程中,表示圆的方程的是( )
| A. | x2+2x+y2-4y+7=0 | B. | $\left\{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}\right.$(0≤θ≤2π) | ||
| C. | ρ=5cosθ | D. | ρ2cos2θ=1 |
