题目内容

17．已知集合M={x|$\frac{x-2}{x+1}$＜0}，N={x|x≤-1}，则集合{x|x≥2}等于（　　）
A．M∩NB．M∪NC．∁R（M∩N）D．∁R（M∪N）

分析 先化简集合M，再根据集合的并集运算求出M∪N={x|x＜2}，这时发现{x|x＜2}∪{x|x≥2}=R，问题得以解决．

解答 解：∵M={x|$\frac{x-2}{x+1}$＜0}={x|-1＜x＜2}，N={x|x≤-1}，
∴M∪N={x|x＜2}，
∴∁R（M∪N）={x|x≥2}，
故选：D．

点评 此题考查的分式不等式的解法及集合间的交、并、补运算是高考中的常考内容，要认真掌握，并确保得分．

练习册系列答案
相关题目
7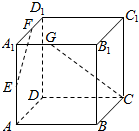．如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AA1，A1D1，A1B1的中点，则异面直线EF与CG所成的角等于（　　）
A．30°B．45°C．60°D．90°
8．f （x）是定义在R上的以2为周期的奇函数，f （3）=0，则函数y=f （x）在区间（-2，5）内的零点个数为（　　）
A．6B．5C．4D．3
5．在区间[-5，5]内随机地取出一个数a，使得1∈{x|2x2+ax-a2＞0}的概率为（　　）
A．$\frac{3}{10}$B．$\frac{3}{20}$C．$\frac{3}{5}$D．$\frac{1}{2}$
12．已知点C在圆O直径BE的延长线上，CA切圆O于点F，DC是∠ACB的平分线交AE于点F，交AB于点D，则∠ADF的度数为45°．
2．已知函数f（x）=3sin（ωx-$\frac{π}{6}$）+1（ω＞0）和g（x）=cos（2x+φ）-2的图象的对称轴完全相同，当x∈[0，$\frac{π}{2}$]时，函数f（x）的值域是[-$\frac{1}{2}$，4]．
9．在△ABC中内角A、B、C所对边分别是a、b、c，若sin2$\frac{B}{2}$=$\frac{c-a}{2c}$，△ABC的形状一定是直角三角形．
6．命题“若x=1，则x2=1”的否命题是（　　）
A．若x=1，则x2≠1B．若x≠1，则x2=1C．若x≠1，则x2≠1D．若x2≠1，则x≠1
7．如图是一个几何体的三视图．则该几何体的体积为（　　）
A．6πB．8πC．12πD．24π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网