题目内容
12. 已知点C在圆O直径BE的延长线上,CA切圆O于点F,DC是∠ACB的平分线交AE于点F,交AB于点D,则∠ADF的度数为45°.
已知点C在圆O直径BE的延长线上,CA切圆O于点F,DC是∠ACB的平分线交AE于点F,交AB于点D,则∠ADF的度数为45°.
分析 根据直径上的圆周角是直角、弦切角定理以及三角形内内角和定理等通过角的关系求解.
解答 解:设∠EAC=α,根据弦切角定理,∠ABE=α.
根据三角形外角定理,∠AEC=90°+α.
根据三角形内角和定理,∠ACE=90°-2α.
由于CD是∠ACB的内角平分线,所以FCE=45°-α.
再根据三角形内角和定理,∠CFE=180°-(90°+α)-(45°-α)=45°.
根据对顶角定理,∠AFD=45°.
由于∠DAF=90°,所以∠ADF=45°.
故答案为:45°.
点评 本题的涉及很独到,试题涉及成动态的,即点C是可变的,在这个动态中求解其中的一个不变量.解决这类试题要善于抓住主要的变化关系,如本题中主要的变量就是∠AEC,抓住这个变量后,其余的角可以使用这个变量进行表达,通过各个角的关系证明求解的目标与这个变量没有关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知集合M={x|$\frac{x-2}{x+1}$<0},N={x|x≤-1},则集合{x|x≥2}等于( )
| A. | M∩N | B. | M∪N | C. | ∁R(M∩N) | D. | ∁R(M∪N) |
4.已知△ABC的内角A、B、C所对的边分别为a、b、c,asinA+csinC-$\sqrt{2}$asinC=bsinB.
(Ⅰ)求B;
(Ⅱ)若C=$\frac{5π}{12}$,b=2,求a和c.
(Ⅰ)求B;
(Ⅱ)若C=$\frac{5π}{12}$,b=2,求a和c.
1.已知数列{an}满足an+1=2an(n∈N*),其前n项和为Sn,则$\frac{S_5}{a_5}$=( )
| A. | $\frac{15}{16}$ | B. | $\frac{31}{16}$ | C. | $\frac{15}{32}$ | D. | $\frac{31}{32}$ |
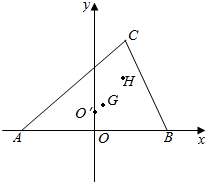 如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按照如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按照上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.
从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按照如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按照上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.