题目内容
2.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)+1(ω>0)和g(x)=cos(2x+φ)-2的图象的对称轴完全相同,当x∈[0,$\frac{π}{2}$]时,函数f(x)的值域是[-$\frac{1}{2}$,4].分析 由条件利用三角函数的周期性求得ω的值,可得函数f(x)的解析式,再利用正弦函数的定义域和值域,求得函数f(x)的值域.
解答 解:函数f(x)=3sin(ωx-$\frac{π}{6}$)+1(ω>0)和g(x)=cos(2x+φ)-2的图象的对称轴完全相同,
故它们的周期相同,即$\frac{2π}{ω}$=$\frac{2π}{2}$,
∴ω=2,f(x)=3sin(2x-$\frac{π}{6}$)+1.
当x∈[0,$\frac{π}{2}$]时,2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴函数f(x)的值域为[-$\frac{3}{2}$+1,4],
即函数f(x)的值域是[-$\frac{1}{2}$,4],
故答案为:[-$\frac{1}{2}$,4].
点评 本题主要考查三角函数的周期性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.(普通中学做)已知数列{an}满足a1+3a2+5a3+…+(2n-1)an=(n-1)3n+1+3(n∈N*),则数列{an}的前n项和Sn=$\frac{3}{2}({3}^{n}-1)$.
10.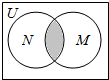 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
17.已知集合M={x|$\frac{x-2}{x+1}$<0},N={x|x≤-1},则集合{x|x≥2}等于( )
| A. | M∩N | B. | M∪N | C. | ∁R(M∩N) | D. | ∁R(M∪N) |
7.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
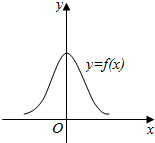

| A. | f(x)=e${\;}^{1-{x}^{2}}$ | B. | f(x)=e${\;}^{{x}^{2}-1}$ | C. | f(x)=e${\;}^{{x}^{2}}$-1 | D. | f(x)=ln(x2-1) |
14.阅读程序框图,为使输出的数据为31,则①处应填的表达式为( )


| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |