题目内容
2.在平面内,$\overrightarrow{A{B_1}}⊥\overrightarrow{A{B_2}},|\overrightarrow{O{B_1}}|=3,|\overrightarrow{O{B_2}}|=4,\overrightarrow{AP}=\overrightarrow{A{B_1}}+\overrightarrow{A{B_2}}$,若$1<|\overrightarrow{OP}|<2$,则$|\overrightarrow{OA}|$的取值范围是( )| A. | $(2\sqrt{3},\sqrt{17})$ | B. | $(\sqrt{17},\sqrt{21})$ | C. | $(\sqrt{17},2\sqrt{6})$ | D. | $(\sqrt{21},2\sqrt{6})$ |
分析 建立坐标系,设B1(a,0),B2(0,b),则P(a,b),O(x,y),利用已知条件向量的模,以及$1<|\overrightarrow{OP}|<2$,转化求解$|\overrightarrow{OA}|$的取值范围即可.
解答 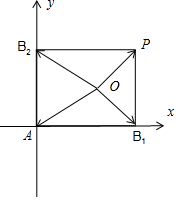 解:由$\overrightarrow{A{B_1}}⊥\overrightarrow{A{B_2}},|\overrightarrow{O{B_1}}|=3,|\overrightarrow{O{B_2}}|=4,\overrightarrow{AP}=\overrightarrow{A{B_1}}+\overrightarrow{A{B_2}}$,如图:建立坐标系,
解:由$\overrightarrow{A{B_1}}⊥\overrightarrow{A{B_2}},|\overrightarrow{O{B_1}}|=3,|\overrightarrow{O{B_2}}|=4,\overrightarrow{AP}=\overrightarrow{A{B_1}}+\overrightarrow{A{B_2}}$,如图:建立坐标系,
设B1(a,0),B2(0,b),则P(a,b),O(x,y),
可得:$\left\{\begin{array}{l}{\sqrt{(x-a)^{2}+{y}^{2}}=3}\\{\sqrt{{x}^{2}+(y-b)^{2}}=4}\end{array}\right.$,
可得(x-a)2+(y-b)2+x2+y2=9+16=25,
$|\overrightarrow{OP}|$=$\sqrt{(x-a)^{2}+(y-b)^{2}}$=$\sqrt{25-({x}^{2}+{y}^{2})}$,
又$|\overrightarrow{OA}|$=$\sqrt{{x}^{2}+{y}^{2}}$,$|\overrightarrow{OP}|$=$\sqrt{25-|\overrightarrow{OA}{|}^{2}}$∈(1,2),
∴1$<25-{\overrightarrow{OA}}^{2}<4$,⇒21$<{\overrightarrow{OA}}^{2}<24$⇒$\sqrt{21}<|\overrightarrow{OA}|<2\sqrt{6}$.
故选:D.
点评 本题考查向量在几何中的应用,向量的模的求法,考查转化思想以及数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{{2\sqrt{5}π}}{5}$ | B. | $\frac{{4\sqrt{5}π}}{5}$ | C. | $\frac{{2\sqrt{10}π}}{5}$ | D. | $\frac{{4\sqrt{10}π}}{5}$ |
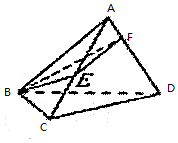 如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.
如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.