题目内容
12.已知函数f(x)=aex•cosx-xsinx,且曲线y=f(x)在(0,f(0))处的切线与x-y=0平行.(1)求a的值;
(2)当$x∈[{-\frac{π}{2},\frac{π}{2}}]$时,试探究函数y=f(x)的零点个数,并说明理由.
分析 (1)利用f′(0)=1,求a的值;
(2)当$x∈[{-\frac{π}{2},\frac{π}{2}}]$时,分类讨论,确定函数的单调性,即可探究函数y=f(x)的零点个数.
解答 解:(1)f′(x)=aex•(cosx-sinx)-sinx-xcosx,
∵f′(0)=1,∴a=1;
(2)①x∈[-$\frac{π}{2}$,0],f′(x)=(ex-x)cosx-(ex+1)sinx,(ex-x)cosx≥0,
(ex+1)sinx≤0,函数单调递增,
∴f(x)在[-$\frac{π}{2}$,0]上至多只有一个零点,
∵f(0)=1>0,f(-$\frac{π}{2}$)=-$\frac{π}{2}$<0,
∴f(x)在[-$\frac{π}{2}$,0]上只有一个零点,
②x∈[0,$\frac{π}{4}$],f(x)>0恒成立,证明如下:
设g(x)=ex-x,则g′(x)=ex-1≥0,函数单调递增,
此时g(x)>g(0)=0,ex>x,cosx≥sinx>0,
∴ex•cosx>xsinx,∴f(x)>0,函数无零点;
③x∈($\frac{π}{4}$,$\frac{π}{2}$],f′(x)=ex•(cosx-sinx)-sinx-xcosx<0,函数单调递减,
∴f(x)在($\frac{π}{4}$,$\frac{π}{2}$]上至多只有一个零点,
∵f($\frac{π}{4}$)>0,f($\frac{π}{2}$)=-$\frac{π}{2}$<0,
∴f(x)在($\frac{π}{4}$,$\frac{π}{2}$]上只有一个零点,
综上所述,当$x∈[{-\frac{π}{2},\frac{π}{2}}]$时,函数有两个零点.
点评 本题考查导数知识的运用,考查函数的零点,考查函数的单调性,考查分类讨论的数学思想,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | $(2\sqrt{3},\sqrt{17})$ | B. | $(\sqrt{17},\sqrt{21})$ | C. | $(\sqrt{17},2\sqrt{6})$ | D. | $(\sqrt{21},2\sqrt{6})$ |
| A. | $\frac{1}{3}$或$\sqrt{10}$ | B. | $\sqrt{10}$或$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{10}$ |
| A. | 任一事件的概率总在(0,1)内 | B. | 不可能事件的概率不一定为0 | ||
| C. | 必然事件的概率一定为1 | D. | 概率为0的事件一定是不可能事件 |
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | ±$\frac{\sqrt{3}}{3}$ |
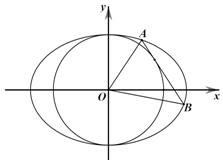 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2