题目内容
17．
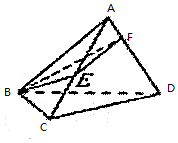如图，在正四面体A-BCD中，所有棱长为1，E，F分别是AC，AD上的动点，求截面△BEF周长的最小值．
分析 首先，展开三棱锥，然后，两点间的连接线BB'即是截面周长的最小值，然后，求解其距离即可．
解答 解：把正四面体A-BCD的侧面展开，
两点间的连接线BB'即是截面周长的最小值．
∵AB=AB′=1，∠BAB′=120°，
∴截面周长最小值是BB’=$\sqrt{1+1-2×1×1×（-\frac{1}{2}）}$=$\sqrt{3}$．
点评 本题重点考查了空间中的距离最值问题，属于中档题．注意等价转化思想的灵活运用．
练习册系列答案
一本好题口算题卡系列答案
相关题目
如图所示，PA⊥平面ABCD，底面ABCD为菱形，$∠ABC=\frac{π}{3}$，PA=AB=4，AC交BD于O，点N是PC的中点．
11．设函数f（x）=e2x+ax在（0，+∞）上单调递增，则实数a的取值范围为（ ）
| A． | [-1，+∞） | B． | （-1，+∞） | C． | [-2，+∞） | D． | （-2，+∞） |
2．在平面内，$\overrightarrow{A{B_1}}⊥\overrightarrow{A{B_2}}，|\overrightarrow{O{B_1}}|=3，|\overrightarrow{O{B_2}}|=4，\overrightarrow{AP}=\overrightarrow{A{B_1}}+\overrightarrow{A{B_2}}$，若$1＜|\overrightarrow{OP}|＜2$，则$|\overrightarrow{OA}|$的取值范围是（ ）
| A． | $（2\sqrt{3}，\sqrt{17}）$ | B． | $（\sqrt{17}，\sqrt{21}）$ | C． | $（\sqrt{17}，2\sqrt{6}）$ | D． | $（\sqrt{21}，2\sqrt{6}）$ |