题目内容
11.点M为棱长是2$\sqrt{2}$的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点N为B1C1的中点,若满足DM⊥BN,则动点M的轨迹的长度为( )| A. | $\frac{{2\sqrt{5}π}}{5}$ | B. | $\frac{{4\sqrt{5}π}}{5}$ | C. | $\frac{{2\sqrt{10}π}}{5}$ | D. | $\frac{{4\sqrt{10}π}}{5}$ |
分析 取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,可得NB⊥面DCH,即动点M的轨迹就是平面DCH与内切球O的交线,求得截面圆的半径r=$\sqrt{{R}^{2}-{d}^{2}}=\frac{2\sqrt{2}}{\sqrt{5}}$,动点M的轨迹的长度为截面圆的周长2πr
解答 解:如图,正方体ABCD-A1B1C1D1的内切球O的半径R=$\sqrt{2}$,由题意,取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,∴NB⊥面DCH,
∴动点M的轨迹就是平面DCH与内切球O的交线,∵正方体ABCD-A1B1C1D1的棱长是2$\sqrt{2}$,∴O到平面DCH的距离为d=$\frac{2}{\sqrt{5}}$,
截面圆的半径r=$\sqrt{{R}^{2}-{d}^{2}}=\frac{2\sqrt{2}}{\sqrt{5}}$,动点M的轨迹的长度为截面圆的周长2πr=$\frac{4\sqrt{10}}{5}$.
故选:D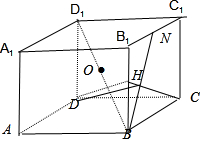
点评 本题考查了空间动点轨迹问题,弄清动点的轨迹是解题关键,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在平面内,$\overrightarrow{A{B_1}}⊥\overrightarrow{A{B_2}},|\overrightarrow{O{B_1}}|=3,|\overrightarrow{O{B_2}}|=4,\overrightarrow{AP}=\overrightarrow{A{B_1}}+\overrightarrow{A{B_2}}$,若$1<|\overrightarrow{OP}|<2$,则$|\overrightarrow{OA}|$的取值范围是( )
| A. | $(2\sqrt{3},\sqrt{17})$ | B. | $(\sqrt{17},\sqrt{21})$ | C. | $(\sqrt{17},2\sqrt{6})$ | D. | $(\sqrt{21},2\sqrt{6})$ |
19.抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB=$\frac{π}{2}$.设线段AB的中点M在l上的投影为N,则$\frac{{|{AB}|}}{{|{MN}|}}$的最小值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
16.已知f(x)=x3-ax在(-∞,-1]上是单调函数,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
3.若实数数列:-1,a1,a2,a3,-81成等比数列,则圆锥曲线x2+$\frac{{y}^{2}}{{a}_{2}}$=1的离心率是( )
| A. | $\frac{1}{3}$或$\sqrt{10}$ | B. | $\sqrt{10}$或$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{10}$ |
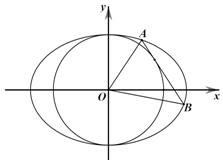 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2