题目内容
按照如图的程序运行，已知输入x的值为2+log23，则输出y的值为（ ）
| A、7 | B、11 | C、12 | D、24 |
考点：程序框图
专题：计算题,算法和程序框图
分析：算法的功能是求y=
的值，根据x的值为2+log23＜4，代入计算可得答案．
|
解答：
解：由程序框图知：算法的功能是求y=
的值，
∵x=2+log23＜2+log24=4，
∴y=22+log23+1=23•3=24．
故选：D．
|
∵x=2+log23＜2+log24=4，
∴y=22+log23+1=23•3=24．
故选：D．
点评：本题考查了选择结构的程序框图，根据框图流程判断算法的功能是解答此类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，则f（已知A（2，1），B（1，-2），C（
，-
），动点P（a，b）满足0≤
•
≤2且0≤
•
≤2，则点P到点C的距离大于
的概率为（ ）
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 4 |
A、1-
| ||
B、
| ||
C、1-
| ||
D、
|
已知双曲线
-
=1(a＞0，b＞0)的左右焦点分别为F1，F2，点O为坐标原点，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则|OA|与|OB|的长度依次为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、a，a | ||||
B、a，
| ||||
C、
| ||||
D、
|
已知集合A={x|x2-2x＜0}，B={x|x≤-1或x＞1}，则A∩（∁RB）=（ ）
| A、{x|0＜x＜1} |
| B、{x|1≤x＜2} |
| C、{x|0＜x≤1} |
| D、{x|1＜x＜2} |
已知中心在原点的双曲线，其右焦点为F（3，0），且F到其中一条渐近线的距离为
，则该双曲线的方程为（ ）
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
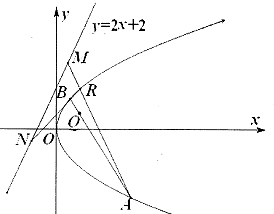已知抛物线C的方程为y2=2px（p＞0），点R（1，2）在抛物线C上．
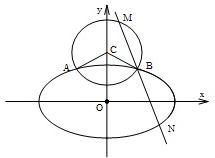已知离心率为