题目内容
已知函数f(x)=log2x与函数g(x)的图象关于y=x对称,且有g(a)g(b)=2,a>0,b>0,则
+
的最小值为( )
| 4 |
| a |
| 1 |
| b |
| A、9 | ||
B、
| ||
| C、4 | ||
| D、5 |
考点:基本不等式
专题:不等式的解法及应用
分析:利用互为反函数的意义可得可得g(x)=2x,再利用指数的运算法则可得a+b=1,利用基本不等式的性质即可得出.
解答:
解:∵函数f(x)=log2x与函数g(x)的图象关于y=x对称,
∴g(x)=2x.
∵g(a)g(b)=2,∴2a•2b=2,∴a+b=1.
又a>0,b>0,
∴(a+b)(
+
)=5+
+
≥5+2
=9.当且仅当a=2b=
时取等号.
∴
+
的最小值为9.
故选:A.
∴g(x)=2x.
∵g(a)g(b)=2,∴2a•2b=2,∴a+b=1.
又a>0,b>0,
∴(a+b)(
| 4 |
| a |
| 1 |
| b |
| 4b |
| a |
| a |
| b |
|
| 1 |
| 2 |
∴
| 4 |
| a |
| 1 |
| b |
故选:A.
点评:本题考查了互为反函数的意义、指数的运算法则、基本不等式的性质等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
在△ABC中,三边长分别为a,b,c,且A=30°,B=45°,a=1,则b的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以双曲线x2-y2=2的右焦点为圆心,且与其渐近线相切的圆的方程是( )
| A、x2+y2-4x-2=0 |
| B、x2+y2-4x+2=0 |
| C、x2+y2+4x-2=0 |
| D、x2+y2+4x+2=0 |
 已知数列{an}的各项均为正数,执行程序框图(如图),当k=4时,S=
已知数列{an}的各项均为正数,执行程序框图(如图),当k=4时,S=| 1 |
| 3 |
| A、2012 | B、2013 |
| C、2014 | D、2015 |
设全集U={x|0<x<2},集合A={x|0<x≤1},则集合∁UA=( )
| A、(0,1) |
| B、(0,1] |
| C、(1,2) |
| D、[1,2) |
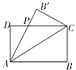 某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为
某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为