题目内容
设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,①
⇒m⊥α,②
⇒α⊥β,③
⇒m∥n,④
⇒m∥n.其中为假命题的是( )
|
|
|
|
| A、①和② | B、②和③ |
| C、③和④ | D、①和④ |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①
⇒m与α相交、平行或m?α,故①是假命题;
②
⇒α⊥β,由平面与平面垂直的判定定理得②是真命题;
③
⇒m∥n,由直线与平面垂直的性质定理得③是真命题;
④
⇒m与n平行或异面,故④是假命题.
故选:D.
|
②
|
③
|
④
|
故选:D.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知a>b,c>d,则下列不等式成立的是( )
| A、b+d<a+c | ||||
| B、ac>bd | ||||
C、
| ||||
| D、a-c>b-d |
已知平面向量
=(1,2),
=(-2,k),若
与
共线,则|3
+
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | ||
| B、4 | ||
C、
| ||
| D、5 |
已知向量
=(-2,-6),|
|=
,
•
=10,则向量
与
的夹角为( )
| a |
| b |
| 10 |
| a |
| b |
| a |
| b |
| A、150° | B、-30° |
| C、120° | D、60° |
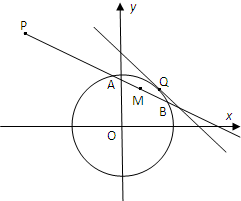 过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.
过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.