题目内容
已知定义域为R的函数f(x)=a-
(a∈R)是奇函数.
(1)求a的值;
(2)判断函数f(x)在R上的单调性,并证明你的结论;
(3)求函数f(x)的值域.
| 2 |
| 3x+1 |
(1)求a的值;
(2)判断函数f(x)在R上的单调性,并证明你的结论;
(3)求函数f(x)的值域.
考点:函数单调性的判断与证明,函数的值域,函数奇偶性的性质
专题:函数的性质及应用
分析:本题(1)利用函数的奇偶性的定义得到关于x的恒等式,从而求出参数a的值,或者利用特殊情况求出参数的值,再用函数奇偶性定义法进行证明;(2)本题可以运用函数单调性定义证明,得到本题结论;(3)利用已知指数函数的值域,求出原函数的值域,得到本题结论.
解答:
解:(1)若存在实数a使函数f(x)为R上的奇函数,则f(0)=0,
∴a=1.
下面证明a=1时f(x)=1-
是奇函数,
∵f(-x)=1-
=1-
=-1+
=-f(x),
∴f(x)=1-
是R上的奇函数.
∴存在实数a=1,使函数f(x)为R上的奇函数.
(2)函数f(x)在R上的增函数.
证明:设x1,x2∈R且设x1<x2,则
f(x1)-f(x2)=
-
=
,
∵y=3x在R上是增函数,且x1<x2,
∴3x1<3x2且(3 x1+1)(3 x2+1)>0,
则f(x1)<f(x2).
∴f(x)是R上的增函数.
(3)f(x)=1-
中
∵3x+1∈(1,+∞),
∴
∈(0,2),
∴1-
∈(-1,1).
∴函数f(x)的值域为:(-1,1).
∴a=1.
下面证明a=1时f(x)=1-
| 2 |
| 3x+1 |
∵f(-x)=1-
| 2 |
| 3-x+1 |
| 2•3x |
| 1+3x |
| 2 |
| 1+3x |
∴f(x)=1-
| 2 |
| 3x+1 |
∴存在实数a=1,使函数f(x)为R上的奇函数.
(2)函数f(x)在R上的增函数.
证明:设x1,x2∈R且设x1<x2,则
f(x1)-f(x2)=
| 2 |
| 3x2+1 |
| 2 |
| 3x1+1 |
| 3(3x1-3x2) |
| (3x1+1)(3x2+1) |
∵y=3x在R上是增函数,且x1<x2,
∴3x1<3x2且(3 x1+1)(3 x2+1)>0,
则f(x1)<f(x2).
∴f(x)是R上的增函数.
(3)f(x)=1-
| 2 |
| 3x+1 |
∵3x+1∈(1,+∞),
∴
| 2 |
| 3x+1 |
∴1-
| 2 |
| 3x+1 |
∴函数f(x)的值域为:(-1,1).
点评:本题考查了函数的奇偶性、单调性和函数的值域,本题难度不大,属于基础题.

练习册系列答案
相关题目
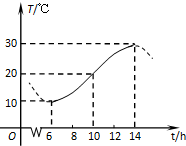 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中ω>0,
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中ω>0,| π |
| 2 |
| A、30℃ | B、27℃ |
| C、25℃ | D、24℃ |
下列说法正确的个数为( )
(1)高一、一班个子高的学生可以构成集合;
(2)2,3,
,|-
|,-0.5这些数组成的集合有5个元素;
(3)集合{x|xy<0,x,y∈R}是指第二和第四象限内的点集.
(1)高一、一班个子高的学生可以构成集合;
(2)2,3,
| 6 |
| 4 |
| 1 |
| 2 |
(3)集合{x|xy<0,x,y∈R}是指第二和第四象限内的点集.
| A、0个 | B、1个 | C、2个 | D、3个 |
