题目内容
12.在等比数列{an}中,2a3-a1a5=0,数列{bn}的通项bn=log4(a2n),Sn=$\frac{n(n-1)}{2}$.n∈N*.(1)求数列{an}与{bn}的通项公式;
(2)数列{an}的前n项和为Tn,求满足不等式Tn<3bn(n∈N*)成立的n的值.
分析 (1)通过数列{an}为等比数列即及2a3-a1a5=0可知a3=2,通过b2=S2-S1=log4(a4)计算可知a4=${4}^{{b}_{2}}$=4,进而可知数列{an}的公比q,计算即得结论;
(2)通过(1)可知Tn=2n-1-$\frac{1}{2}$,问题转化为解不等式2n-1-$\frac{1}{2}$<3(n-1),计算即得结论.
解答 解:(1)∵数列{an}为等比数列,
∴2a3-a1a5=0,即2a3-a3a3=0,
∴a3=2或a3=0(舍),
∵Sn=$\frac{n(n-1)}{2}$,
∴b2=S2-S1=1-0=1,
又∵b2=log4(a4),
∴a4=${4}^{{b}_{2}}$=4,
∴数列{an}的公比q=$\frac{{a}_{4}}{{a}_{3}}$=$\frac{4}{2}$=2,
∴an=${a}_{3}•{q}^{n-3}$=2n-2,
∴bn=log4(a2n)=$lo{g}_{4}{2}^{2n-2}$=n-1;
(2)由(1)可知Tn=$\frac{\frac{1}{2}(1-{2}^{n})}{1-2}$=2n-1-$\frac{1}{2}$,
∴Tn<3bn(n∈N*)成立即2n-1-$\frac{1}{2}$<3(n-1)成立,
∴2n-1-3n<-$\frac{5}{2}$,
∴n=2、3、4.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
17.已知x,y满足(x-1)2+y2=16,则x2+y2的最大值为( )
| A. | 3 | B. | 5 | C. | 9 | D. | 25 |
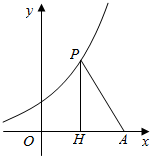 如图,已知点A(10,0),直线x=t(0<t<10)与函数y=ex+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).
如图,已知点A(10,0),直线x=t(0<t<10)与函数y=ex+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).