Question

3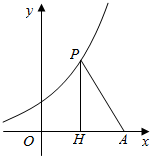．如图，已知点A（10，0），直线x=t（0＜t＜10）与函数y=e^x+1的图象交于点P，与x轴交于点H，记△APH的面积为f（t）．
（Ⅰ）求函数f（t）的解析式；
（Ⅱ）求函数f（t）的最大值．

Answer 1

分析 （ I）由题意设点P坐标，来表示AH，PH的大小，计算出△APH的面积f（t）=$\frac{1}{2}$•AH•PH；
（ II）求f（t）的导函数f，（t），令f'（t）=0，求得f'（t）＞0、＜0的t的取值范围，从而求得f（t）的最大值．

解答 解：（ I）由已知AH=10-t，PH=e^t+1
所以△APH的面积为$f（t）=\frac{1}{2}（10-t）{e^{t+1}}，0＜t＜10$．
（ II）解：$f'（t）=-\frac{1}{2}{e^{t+1}}+\frac{1}{2}×（10-t）×{e^{t+1}}={e^{t+1}}（5-t）$，
令f'（t）=0，解得得t=5，
函数f（t）与f'（t）在定义域上的情况下表：

t	（0，5）	5	（5，10）
f'（t）	+	0	-
f（t）	↗	极大值	↘

所以当t=5时，函数f（t）取得最大值$t=\frac{5}{2}{e^6}$．

点评 本题考查了函数的综合应用，其中有利用导数来求函数在某一区间上的最值问题，属于中档题．