题目内容
若关于x的方程
=kx2有四个不同的实数解,则k的取值范围为( )
| |x| |
| x+4 |
| A、(0,1) | ||
B、(
| ||
C、(
| ||
| D、(1,+∞) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:欲使方程
=kx2有四个不同的实数解,当x=0时,是方程的1个根,则只要方程
=kx2有3个不同的实数解,
=
,结合函数g(x)=
的图象可求.
| |x| |
| x+4 |
| |x| |
| x+4 |
| 1 |
| k |
|
|
解答:
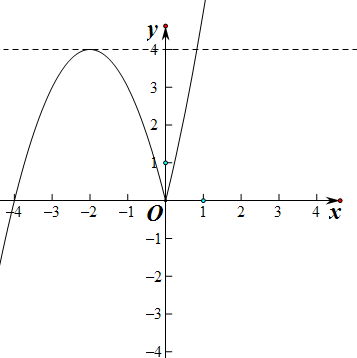 解:要使方程
解:要使方程
=kx2有四个不同的实数解,
当x=0时,是方程的1个根,
所以只要方程
=kx2有3个不同的实数解,
变形得
=
,设函数g(x)=
,
如图
所以只要0<
<4即可,
所以k>
;
故选C.
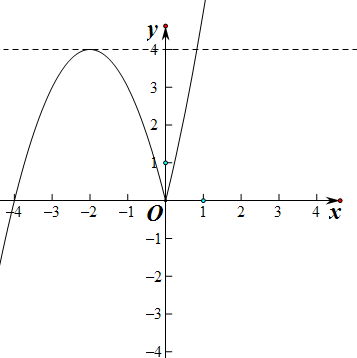 解:要使方程
解:要使方程| |x| |
| x+4 |
当x=0时,是方程的1个根,
所以只要方程
| |x| |
| x+4 |
变形得
| 1 |
| k |
|
|
如图
所以只要0<
| 1 |
| k |
所以k>
| 1 |
| 4 |
故选C.
点评:本题考查了函数的图象的交点与方程根的关系,考查了数形结合解决方程根的个数问题,关键是准确构造函数,准确画出图象,经常考查,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
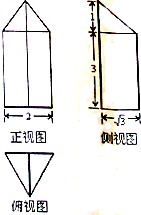

A、2
| ||||
B、4
| ||||
C、
| ||||
D、
|
函数f(x)=
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
-2,e6+
-2)
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
|
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
| 1 |
| e |
| 1 |
| e2 |
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
球的半径为2,它的内接正方体的表面积为( )
| A、8 | B、16 | C、32 | D、64 |
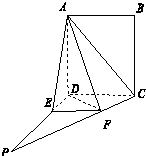 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=AD,AF⊥PC于点F,FE∥CD交PD于点E.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=AD,AF⊥PC于点F,FE∥CD交PD于点E.