题目内容

计算：2cos
π
2
-tan
π
4
+
3
4
tan2
π
6
-sin
π
6
+cos2
π
6
+sin
3π
2
．
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：运用特殊角的三角函数值，即可化简得到．
解答： 解：2cos
π
2
-tan
π
4
+
3
4
tan2
π
6
-sin
π
6
+cos2
π
6
+sin
3π
2

=2×0-1+
3
4
×(
3
3
)2-
1
2
+（
3
2
）2+（-1）
=-1+
3
4
×
1
3
-
1
2
+
3
4
-1
=-
3
2
．
点评：本题考查三角函数的求值，考查特殊角的三角函数值，熟记它们是迅速解题的关键，属于基础题．
练习册系列答案
相关题目
如图1，在矩形ABCD中，AB=3，AD=
3
，E为CD边上的点，且EC=2DE，AE与BD相交于点O，现沿AE将△ADE折起，连接DB，DC得到如图2所示的几何体．

（1）求证：AE⊥平面DOB；
（2）当平面ADE⊥平面ABCE时，求二面角A-DE-B的余弦值．
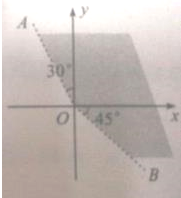如图，终边落在OA位置的角α的集合是
 
；终边落在OB位置，且在-360°～360°内的角α的集合是
 
；终边落在阴影部分（不含边界）的角α的集合是
 
．
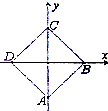如图，正方形ABCD的边长为2，分别以DB，AC所在直线为x，y轴建立直角坐标系，用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′，则四边形A′B′C′D′的面积为
 
．
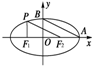如图，椭圆的中心在原点，焦点F1、F2在x轴上，A、B是椭圆的顶点，P是椭圆上一点，且
PF1⊥x轴，PF2∥AB，则此椭圆的离心率是（　　）
A、
1
2
B、
1
3
C、
5
5
D、
2
2
若关于x的方程
|x|
x+4
=kx2有四个不同的实数解，则k的取值范围为（　　）
A、（0，1）
B、(
1
4
，1)
C、(
1
4
，+∞)
D、（1，+∞）
下列命题：
①（
a
）2•（
a
）2=|
a
|4；
②（
a
•
b
）•
c
=（
a
•
c
）•
b
；
③|
a
•
b
|=|
a
|•|
b
|；
④若
a
∥
b
，
b
∥
c
，则
a
∥
c
；
⑤
a
∥
b
，则存在唯一实数λ，使
b
=λ
a
；
⑥若
a
•
c
=
b
•
c
，且
c
≠
0
，则
a
=
b
；
⑦设
e1
，
e2
是平面内两向量，则对于平面内任何一向量
a
，都存在唯一一组实数x、y，使
a
=x
e1
+y
e2
成立；
⑧若
a
•
b
=0，则
a
=
0
或
b
=
0
．
真命题的题号为
 
．
已知0＜a＜1，则在同一坐标系中，函数y=a-x与y=logax的图象是（　　）
A、
B、
C、
D、
设数列{an}的前n项和为Sn，且a1=2，an+1=2Sn+2．
（1）求数列{an}的通项公式；
（2）若数列{bn}的各项均为正数，且bn是
n
an
与
n
an+2
的等比中项，求bn的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网