题目内容
奇函数f(x)满足f(x+4)=f(x),且当x∈(-2,0]时,f(x)=log2(1-x),求f(2013)的值.
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:奇函数f(x)满足f(x+4)=f(x),则f(-x)=-f(x),f(x)的最小正周期为4,则f(2013)=f(1),当x∈(-2,0]时,f(x)=log2(1-x),求出f(-1),即可得到f(1).
解答:
解:奇函数f(x)满足f(x+4)=f(x),
则f(-x)=-f(x),f(x)的最小正周期为4,
则f(2013)=f(503×4+1)=f(1),
当x∈(-2,0]时,f(x)=log2(1-x),
则f(-1)=log2(1+1)=1,
即有f(1)=-f(-1)=-1,
则有f(2013)=-1.
则f(-x)=-f(x),f(x)的最小正周期为4,
则f(2013)=f(503×4+1)=f(1),
当x∈(-2,0]时,f(x)=log2(1-x),
则f(-1)=log2(1+1)=1,
即有f(1)=-f(-1)=-1,
则有f(2013)=-1.
点评:本题考查函数的性质和运用,考查函数的周期性和奇偶性及运用,考查运算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
复数
(i是虚数单位)的虚部是( )
| 2i |
| 1+i |
| A、i | B、-i | C、1 | D、-1 |
在正方体ABCD-A1B1C1D1中,直线A1D与直线D1C1所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
若关于x的方程
=kx2有四个不同的实数解,则k的取值范围为( )
| |x| |
| x+4 |
| A、(0,1) | ||
B、(
| ||
C、(
| ||
| D、(1,+∞) |
登上一个四级的台阶,可以选择的方式共有( )种.
| A、3 | B、4 | C、5 | D、8 |
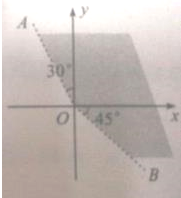 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是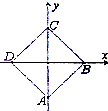 如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为
如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为