题目内容
函数f(x)=
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
-2,e6+
-2)
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
|
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
| 1 |
| e |
| 1 |
| e2 |
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:对于①画出y=f(x)与y=m的图象即可;对于②,结合图象把abcd的不等式用m表示出来
对于③同样用m把a+b+c+d表示出来;对于④若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,画图即可.
对于③同样用m把a+b+c+d表示出来;对于④若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,画图即可.
解答:
解:∵f(x)=
,∴函数f(x)的图象如下

若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①正确
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b是x2+2x+m-3=0
的两根,∴a+b=-2,ab=m-3,∴ab∈[0,1),且lnc=2-m,lnd=2+m,∴ln(cd)=4∴cd=e4,
∴abcd∈[0,e4),∴②是正确的.
由2-lnx=4得x=
,由2-lnx=3得x=
,∴c∈(
,
],又∵cd=e4,
∴a+b+c+d=c+
-2在(
,
]是递减函数,∴a+b+c+d∈[e5+
-2,e6+
-2);
∴③是正确的
若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,
而直线y=-x+3 与y=-x+
均与y=f(x)有三个交点,∴m不唯一.∴④是不正确的
故选A
|

若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①正确
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b是x2+2x+m-3=0
的两根,∴a+b=-2,ab=m-3,∴ab∈[0,1),且lnc=2-m,lnd=2+m,∴ln(cd)=4∴cd=e4,
∴abcd∈[0,e4),∴②是正确的.
由2-lnx=4得x=
| 1 |
| e2 |
| 1 |
| e |
| 1 |
| e2 |
| 1 |
| e |
∴a+b+c+d=c+
| e4 |
| c |
| 1 |
| e2 |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e2 |
∴③是正确的
若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,
而直线y=-x+3 与y=-x+
| 15 |
| 4 |
故选A
点评:本题考查函数的图象,分段函数,零点与方程的根之间的关系,综合性较强.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
若关于x的方程
=kx2有四个不同的实数解,则k的取值范围为( )
| |x| |
| x+4 |
| A、(0,1) | ||
B、(
| ||
C、(
| ||
| D、(1,+∞) |
登上一个四级的台阶,可以选择的方式共有( )种.
| A、3 | B、4 | C、5 | D、8 |
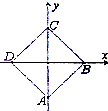 如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为
如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为


