题目内容
已知数列{an}满足a1=1,an+1=an+n+2n(n∈N*),则an等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得an+1-an=n+2n,由此利用累加法能求出an.
解答:
解:∵数列{an}满足a1=1,an+1=an+n+2n(n∈N*),
∴an+1-an=n+2n,
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+1+2+2+22+3+23+4+24+…+(n-1)+2n-1
=1+[1+2+3+4+…+(n-1)]+(2+22+23+24+…+2n-1)
=1+
(1+n-1)+
=
+2n-1.
故选:B.
∴an+1-an=n+2n,
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+1+2+2+22+3+23+4+24+…+(n-1)+2n-1
=1+[1+2+3+4+…+(n-1)]+(2+22+23+24+…+2n-1)
=1+
| n-1 |
| 2 |
| 2(1-2n-1) |
| 1-2 |
=
| n(n-1) |
| 2 |
故选:B.
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意累加法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f(x)在x=a处有导数,则
为( )
| lim |
| h→a |
| f(h)-f(a) |
| h-a |
| A、f(a) | B、f′(a) |
| C、f′(h) | D、f(h) |
已知函数y=f(x)对任意x∈R,恒有(f(x)-sinx)(f(x)-cosx)=0成立,则下列关于函数 y=f(x)的说法正确的是( )
| A、最小正周期是2π |
| B、值域是[-1,1] |
| C、是奇函数或是偶函数 |
| D、以上都不对 |
 如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是( )
如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
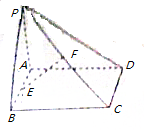 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.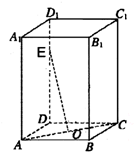 如图,在长方体ABCD-A1B1C1D1中,O为AC的中点,设E是棱DD1上的点,且
如图,在长方体ABCD-A1B1C1D1中,O为AC的中点,设E是棱DD1上的点,且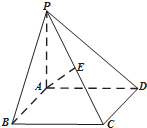 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2