题目内容
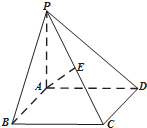 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,由此能求出异面直线BC与AE所成的角.
解答:
解: 以A为原点,AB为x轴,AD为y轴,AP为z轴,
以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
B(2,0,0),C(2,2
,0),P(0,0,2),
A(0,0,0),E(1,
,1),
=(0,2
,0),
=(1,
,1),
设异面直线BC与AE所成的角为θ,
cos<
,
>=
=
=
,
∴异面直线BC与AE所成的角的大小为
.
故选:B.
 以A为原点,AB为x轴,AD为y轴,AP为z轴,
以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
B(2,0,0),C(2,2
| 2 |
A(0,0,0),E(1,
| 2 |
| BC |
| 2 |
| AE |
| 2 |
设异面直线BC与AE所成的角为θ,
cos<
| BC |
| AE |
|
| ||||
|
|
| 4 | ||||
2
|
| ||
| 2 |
∴异面直线BC与AE所成的角的大小为
| π |
| 4 |
故选:B.
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力,解题时要注意向量法的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则|
|的取值范围是( )
| AB |
| A、[0,5] |
| B、[1,5] |
| C、(1,5) |
| D、[1,25] |
已知数列{an}满足a1=1,an+1=an+n+2n(n∈N*),则an等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin
π,4a,cos
π三个数成等比数列,则a=( )
| 5 |
| 6 |
| 11 |
| 3 |
A、-
| ||
B、
| ||
C、-
| ||
| D、0 |
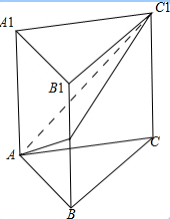 如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为
如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为