题目内容
 如图几何体中,四边形ABCD为矩形,AB=3BC=6,BF=CF=AE=DE=2,EF=4,EF∥AB,G为FC的中点,M为线段CD上的一点,且CM=2.
如图几何体中,四边形ABCD为矩形,AB=3BC=6,BF=CF=AE=DE=2,EF=4,EF∥AB,G为FC的中点,M为线段CD上的一点,且CM=2.(Ⅰ)证明:AF∥面BDG;
(Ⅱ)证明:面BGM⊥面BFC;
(Ⅲ)求三棱锥F-BMC的体积V.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)首先,连接AC交BD于O点,得到OG为△AFC的中位线,从而得到OG∥AF,命题得证;
(Ⅱ)先连接FM,证明BG⊥CF,然后,证明△FCM为正三角形,从而得到CF⊥面BGM,从而命题得证;
(Ⅲ)转化成三棱锥F-BMG和三棱锥C-BMG的体积之和,它们的体积之和就是以FC为高,以BMG为底的三棱锥的体积,从而得到结果.
(Ⅱ)先连接FM,证明BG⊥CF,然后,证明△FCM为正三角形,从而得到CF⊥面BGM,从而命题得证;
(Ⅲ)转化成三棱锥F-BMG和三棱锥C-BMG的体积之和,它们的体积之和就是以FC为高,以BMG为底的三棱锥的体积,从而得到结果.
解答:
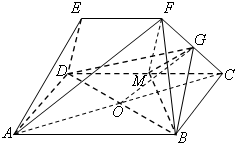 解:(Ⅰ)连接AC交BD于O点,则O为AC的中点,连接OG
解:(Ⅰ)连接AC交BD于O点,则O为AC的中点,连接OG
∵点G为CF中点,
∴OG为△AFC的中位线
∴OG∥AF,
∵AF?面BDG,OG?面BDG,
∴AF∥面BDG,
(Ⅱ)连接FM,
∵BF=CF=BC=2,G为CF的中点,
∴BG⊥CF∵CM=2,
∴DM=4∵EF∥AB,ABCD为矩形,
∴EF∥DM,
又∵EF=4,
∴EFMD为平行四边形
∴FM=ED=2,
∴△FCM为正三角形,
∴MG⊥CF,
∵MG∩BG=G,
∴CF⊥面BGM,
∵CF?面BFC,
∴面BGM⊥面BFC.
(Ⅲ)VF-BMC=VF-BMG+VC-BMG=
×SBMG×FC=
×SBMG×2
∵GM=BG=
,BM=2
∴SBMG=
×2
×1=
∴VF-BMC=
×SBMC=
,
∴三棱锥F-BMC的体积V=
.
 解:(Ⅰ)连接AC交BD于O点,则O为AC的中点,连接OG
解:(Ⅰ)连接AC交BD于O点,则O为AC的中点,连接OG∵点G为CF中点,
∴OG为△AFC的中位线
∴OG∥AF,
∵AF?面BDG,OG?面BDG,
∴AF∥面BDG,
(Ⅱ)连接FM,
∵BF=CF=BC=2,G为CF的中点,
∴BG⊥CF∵CM=2,
∴DM=4∵EF∥AB,ABCD为矩形,
∴EF∥DM,
又∵EF=4,
∴EFMD为平行四边形
∴FM=ED=2,
∴△FCM为正三角形,
∴MG⊥CF,
∵MG∩BG=G,
∴CF⊥面BGM,
∵CF?面BFC,
∴面BGM⊥面BFC.
(Ⅲ)VF-BMC=VF-BMG+VC-BMG=
| 1 |
| 3 |
| 1 |
| 3 |
∵GM=BG=
| 3 |
| 2 |
∴SBMG=
| 1 |
| 2 |
| 2 |
| 2 |
∴VF-BMC=
| 2 |
| 3 |
2
| ||
| 3 |
∴三棱锥F-BMC的体积V=
2
| ||
| 3 |
点评:本题重点考查了面面垂直、线面平行、空间几何体的体积等知识,本题属于中档题.

练习册系列答案
相关题目
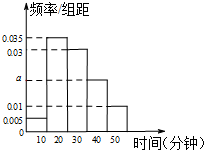 某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到的频率分布直方图如图所示.
某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到的频率分布直方图如图所示.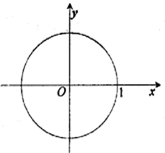 如图在单位圆中,
如图在单位圆中, 在△ABC中,角A,B,C所对的边分别是a,b,c,cosC=-
在△ABC中,角A,B,C所对的边分别是a,b,c,cosC=-