题目内容
14.对角线的长为$\sqrt{3}$的正方体的表面积为6.分析 由对角线的长为$\sqrt{3}$,先求出正方体的棱长,由此能求出正方体的表面积.
解答 解:设正方体的棱长为a,
∵对角线的长为$\sqrt{3}$,
∴$\sqrt{3}a$=$\sqrt{3}$,
解得a=1,
∴正方体的表面积S=6×12=6.
故答案为:6.
点评 本题考查正方体的表面积的求法,是基础题,解题时要认真审题,注意正方体的结构特征的合理运用.

练习册系列答案
相关题目
4.已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=( )
| A. | 2 | B. | -2 | C. | -98 | D. | 98 |
5.已知函数f(x)=$\left\{\begin{array}{l}{|log_2x|,0<x<2}\\{cos(\frac{π}{2}-\frac{π}{4}x),2≤x≤10}\end{array}\right.$,若存在实数x1,x2,x3,x4满足x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则x1x2(x3-1)(x4-1)的取值范围是( )
| A. | ∅ | B. | (9,21) | C. | (21,25) | D. | (9,25) |
9.$在△ABC中,|{\overrightarrow{BC}}|=8,|{\overrightarrow{CA}}|=6,\overrightarrow{BA}•\overrightarrow{CA}$=60,则∠C=( )
| A. | 60° | B. | 30° | C. | 150° | D. | 120° |
6.如图所示,网格纸上小正方形的边长为1cm,粗实线为某空间几何体的三视图,则该几何体的体积为( ) 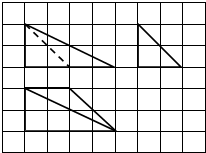

| A. | 2 cm3 | B. | 4 cm3 | C. | 6 cm3 | D. | 8 cm3 |
3.已知圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=( )
| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
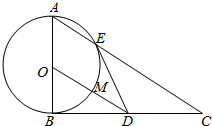 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.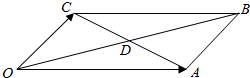 在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).
在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).