��Ŀ����
2����֪����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{3��}{4}$��|$\overrightarrow{a}$|=$\sqrt{2}$��|$\overrightarrow{b}$|=2����$\overrightarrow{a}$•��$\overrightarrow{a}$-2$\overrightarrow{b}$��=6������ ���$\overrightarrow{a}$2��$\overrightarrow{a}•\overrightarrow{b}$����$\overrightarrow{a}$•��$\overrightarrow{a}$-2$\overrightarrow{b}$��չ���ó��𰸣�
��� �⣺$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{2}��2��cos\frac{3��}{4}$=-2��$\overrightarrow{a}$2=|$\overrightarrow{a}$|2=2��
��$\overrightarrow{a}$•��$\overrightarrow{a}$-2$\overrightarrow{b}$��=$\overrightarrow{a}$2-2$\overrightarrow{a}•\overrightarrow{b}$=2+2��2=6��
�ʴ�Ϊ��6��
���� ���⿼����ƽ�����������������㣬���ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
12����֪iΪ������λ������$\frac{2+4i}{i}$=��������
| A�� | 4-2i | B�� | 4+2i | C�� | -4-2i | D�� | -4+2i |
10���躯��f��x���Ƕ�����R�ϵ�ż�������Ҷ������x��R������f��x+2��=f��x������-1��x��0ʱ��f��x��=-x2����ֱ��y=-x+m�뺯��y=f��x����ͼ����������ͬ�Ĺ����㣬��ʵ��m��ֵΪ��������
| A�� | 2k-$\frac{1}{4}$��k��Z�� | B�� | 2k+$\frac{1}{4}$��k��Z�� | C�� | 2k��2k-$\frac{1}{4}$��k��Z�� | D�� | 2k��2k+$\frac{1}{4}$��k��Z�� |
7��2015����������ܴ���������ѧУ�ֱ���3����2����1��ѧ������6��ѧ��Ҫ�ų�һ�ź�Ӱ����ͬУѧ������һ��ĸ����ǣ�������
| A�� | $\frac{1}{30}$ | B�� | $\frac{1}{15}$ | C�� | $\frac{1}{10}$ | D�� | $\frac{1}{5}$ |
11����֪ij�����������ͼ��ͼ��ʾ����ü�����ı������������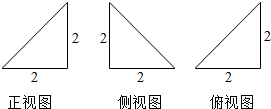

| A�� | 6 | B�� | $6+2\sqrt{3}$ | C�� | $8+8\sqrt{2}$ | D�� | $4+4\sqrt{2}$ |