题目内容
3.已知圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=( )| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
分析 解法一:由题意可得圆C截直线y=2x+b所得线段的长为2,圆心C(1,2)到直线y=2x+b的距离为1,即$\frac{|2×1-2+b|}{\sqrt{5}}$=1,由此求得b的值.
解法二:由题意可得圆心(1,2)到y轴的距离等于圆心(1,2)到直线y=2x+b的距离,即 $\frac{|2×1-2+b|}{\sqrt{5}}$=1,由此求得b的值.
解答 解:解法一:把x=0,代入圆C:(x-1)2+(y-2)2=2,求得y=1,或 y=3,
可得圆截y轴所得线段长为2,
故圆C(x-1)2+(y-2)2=2截直线y=2x+b所得线段的长为2.
故圆心C(1,2)到直线y=2x+b的距离为1,即$\frac{|2×1-2+b|}{\sqrt{5}}$=1,∴b=±$\sqrt{5}$.
故选:D.
解法二:根据圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,
可得圆心(1,2)到y轴的距离等于圆心(1,2)到直线y=2x+b的距离.
而圆心(1,2)到y轴的距离等于为1,故圆心(1,2)到直线y=2x+b的距离也等于1,
即 $\frac{|2×1-2+b|}{\sqrt{5}}$=1,∴b=±$\sqrt{5}$.
故选:D.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11.已知某几何体的三视图如图所示,则该几何体的表面积( )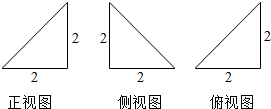

| A. | 6 | B. | $6+2\sqrt{3}$ | C. | $8+8\sqrt{2}$ | D. | $4+4\sqrt{2}$ |
13.Sn表示数列{an}(n≥1)的前n项和,已知a1=1,且?n≥1,Sn+1=4an+2,则a2013等于( )
| A. | 3019•22012 | B. | 3019•22013 | C. | 3018•22012 | D. | 以上答案均不对 |
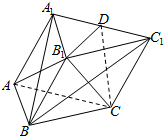 如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.
如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.