题目内容
Rt△ABC中CA=CB=
,M为AB的中点,将△ABC沿CM折叠,使A、B之间的距离为1,则三棱锥M-ABC外接球的表面积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、3π | ||
D、
|
考点:球的体积和表面积
专题:空间位置关系与距离
分析:由已知中得三棱锥M-ABC的底面为边长为1的等边三角形,且MC与底面MAB垂直,故其外接球可转化为以MAB为底面,以MC为高的正三棱柱的外接球,求出球半径后,代入球表面积公式,可得答案.
解答:
解:∵Rt△ABC中CA=CB=
,
∴AB=2,
又∵M为AB的中点,
∴MA=MB=MC=1,
故对折后三棱锥M-ABC的底面为边长为1的等边三角形,
如下图所示:
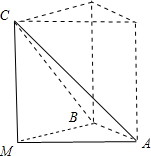
其外接球可化为以MAB为底面,以MC为高的正三棱柱的外接球,
设三棱锥M-ABC外接球的球心为O,
则球心到MAB的距离d=
MC=
,
平面MAB的外接圆半径r=
,
故三棱锥M-ABC外接球的半径R=
=
,
故三棱锥M-ABC外接球的表面积S=4πR2=
,
故选:D
| 2 |
∴AB=2,
又∵M为AB的中点,
∴MA=MB=MC=1,
故对折后三棱锥M-ABC的底面为边长为1的等边三角形,
如下图所示:

其外接球可化为以MAB为底面,以MC为高的正三棱柱的外接球,
设三棱锥M-ABC外接球的球心为O,
则球心到MAB的距离d=
| 1 |
| 2 |
| 1 |
| 2 |
平面MAB的外接圆半径r=
| ||
| 3 |
故三棱锥M-ABC外接球的半径R=
| d2+r2 |
|
故三棱锥M-ABC外接球的表面积S=4πR2=
| 7π |
| 3 |
故选:D
点评:本题考查的知识点是球的体积和表面积,其中根据已知条件求出球的半径是解答本题的关键.

练习册系列答案
相关题目
已知集合A={x∈Z|-1≤x≤1},B={x|x<a},若集合A∩B有且仅有一个元素,则实数a的取值范围是( )
| A、[-1,0) |
| B、(-1,0] |
| C、(-1,0) |
| D、[-1,0] |
已知f(x)=|x+2|+|x-4|的最小值为n,则(x-
)n的展开式中常数项为( )
| 2 |
| x |
| A、-160 | B、-20 |
| C、20 | D、160 |
由函数y=cosx与x=0,x=
π,y=0围成的几何图形的面积为( )
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
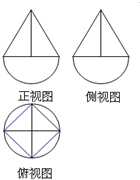 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||||
B、5+
| ||||
C、5+
| ||||
D、
|
已知tan2α=
,α∈(0,
),则
=( )
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
已知f(x)=sinωx+
cosωx(ω>0)的两条相邻的对称轴间的距离为
,且f(x)图象关于点(x0,0)成中心对称,则x0可能为( )
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|