题目内容

球面上有三个点A、B、C，其中AB=18，BC=24，AC=30，且球心到平面ABC的距离为球半径的一半，那么这个球的半径为（　　）
A、20
B、30
C、10
3
D、15
3
考点：球的体积和表面积
专题：空间位置关系与距离
分析：求出三角形ABC的外心，利用球心到△ABC所在平面的距离为球半径的一半，求出球的半径．
解答： 解：由题意AB=18，BC=24，AC=30，∵182+242=302，可知三角形是直角三角形，
三角形的外心是AC的中点，球心到截面的距离就是球心与三角形外心的距离，
设球的半径为R，球心到△ABC所在平面的距离为球半径的一半，
所以R2=（
1
2
R）2+152，
解得R2=300，
∴R=10
3
．
故选：C．
点评：本题是中档题，考查球的内接多面体，找出球的半径满足的条件是解题的关键．
练习册系列答案
相关题目
函数y=a1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny=0（m＞-1，n＞0）上，则
1
m+1
+
1
n
的最小值为
 
．
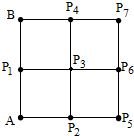如图，四个边长为1的小正方形排成一个大正方形，AB是大正方形的一条边，Pi（i=1，2，…，7）是小正方形的其余顶点，则
AB
•
APi
（i=1，2，…，7）的不同值的个数为（　　）
A、7B、5C、3D、1
下列四个命题中真命题的个数是（　　）
①若y=f（x）是奇函数，则y=|f（x）|的图象关于y轴对称；
②若logm3＜logn3＜0，则0＜m＜n＜1；
③若函数f（x）对任意x∈R满足f（x）•f（x+4）=1，则8是函数f（x）的一个周期；
④命题“在斜△ABC中，A＞B是|tanA|＞|tanB|成立的充要条件；
⑤命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0”．
A、1B、2C、3D、4
如图，PQ是半径为1的圆A的直径，△ABC是边长为1的正三角形，则
BP
•
CQ
的最大值为（　　）
A、
1
2
B、
1
4
C、1
D、2
抛物线x2=4y的焦点到双曲线y2-
x2
4
=1的渐近线的距离等于（　　）
A、
5
B、
5
5
C、
2
5
5
D、
5
2
若3a，b，c成等比数列，则函数f（x）=ax3+bx2+cx+d的零点个数为（　　）
A、0B、1C、2D、3
如图是某空间几何体的直观图，则该几何体的侧视图是（　　）
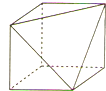
A、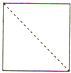
B、
C、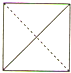
D、
从集合A={1，2，3，4，5}中任取三个元素构成三元有序数组（a1，a2，a3），规定a1＜a2＜a3
（Ⅰ）从所有三元有序数组中任选一个，求它的所有元素之和等于10的概率；
（Ⅱ）定义三元有序数组（a1，a2，a3）的“项标距离”为d=|a1-1|+|a2-2|+|a3-3|，从所有三元有序数组中任选一个，求它的“项标距离”d为偶数的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网