题目内容
曲线y=x3与直线y=x所围成图形的面积为( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
考点:定积分
专题:导数的综合应用
分析:先根据题意画出区域,然后依据图形得到积分下限为0,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可;利用定积分的几何意义求定积分
(x-x2)dx即可.
| ∫ | 1 0 |
解答:
解:解:曲线y=x3与y=x的交点坐标为(0,0),(1,1),(-1,-1)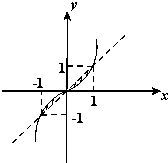
曲线y=x3与直线y=x,
根据题意画出图形,两个图形的交点为:(0,0),(1,1),(-1,-1),直线y=x与曲线y=x3所围成图形的面积为
2
(x-x3)dx=2(
x2-
x4)|
=
;
故选C.

曲线y=x3与直线y=x,
根据题意画出图形,两个图形的交点为:(0,0),(1,1),(-1,-1),直线y=x与曲线y=x3所围成图形的面积为
2
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 4 |
1 0 |
| 1 |
| 2 |
故选C.
点评:本小题考查根据定积分的几何意义,以及会利用定积分求图形面积的能力,同时考查了函数图象的对称性.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
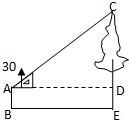 如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )A、(
| ||||||
B、(5
| ||||||
C、
| ||||||
| D、4m |
若x2+y2-x+y-m=0,表示一个圆的方程,则m的取值范围是( )
A、m>-
| ||
B、m≥-
| ||
C、m<-
| ||
| D、m>-2 |
已知
,
均为单位向量,它们的夹角为60°,那么|
+2
|等于( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
 如图:α∩β=AB,PC⊥α,PD⊥β,C、D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.
如图:α∩β=AB,PC⊥α,PD⊥β,C、D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.