题目内容
已知两座灯塔A和B与海洋观察站C的距离分别为a海里和2a海里，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A和B的距离为 海里．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：先根据题意求得∠ACB，进而根据余弦定理求得AB．
解答：
解：依题意知∠ACB=180°-20°-40°=120°，
在△ABC中，由余弦定理知AB=
=
=
a．
即灯塔A与灯塔B的距离为
a．
故答案为：
a
在△ABC中，由余弦定理知AB=
| AC2+BC2-2AC•BC•cos120° |
| 7a2 |
| 7 |
即灯塔A与灯塔B的距离为
| 7 |
故答案为：
| 7 |
点评：本题主要考查了余弦定理的应用．余弦定理可以解决知道两个边和1个角来求令一个边，属于基本知识的考查．
练习册系列答案
相关题目
已知平面向量
，
满足|
|=1，|
|=2，且（
+
）⊥
，则
与
的夹角是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
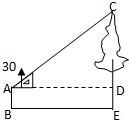如图，小明利用有一个锐角是30°的三角板测量一棵树的高度，已知他与树之间的水平距离BE为5m，AB为1.5m（即小明的眼睛距地面的距离），那么这棵树高是（ ）A、（
| ||||||
B、（5
| ||||||
C、
| ||||||
| D、4m |
如图：α∩β=AB，PC⊥α，PD⊥β，C、D是垂足，试判断直线AB与CD的位置关系？并证明你的结论．若x2+y2-x+y-m=0，表示一个圆的方程，则m的取值范围是（ ）
A、m＞-
| ||
B、m≥-
| ||
C、m＜-
| ||
| D、m＞-2 |
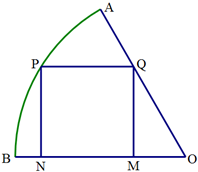如图，在半径为