题目内容
已知a,b为两条直线,α,β为两个平面,下列命题中正确的是( )
| A、若α∥b,β∥b,则α∥β |
| B、若α∥a,α∥b,则a∥b |
| C、若a⊥α,b⊥β,则α∥β |
| D、若a⊥α,a⊥β,则α∥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:若α∥b,β∥b,则α与β相交或平行,故A错误;
若α∥a,α∥b,则a与b相交、平行或异面,故B错误;
若a⊥α,b⊥β,则α与β相交或平行,故C错误;
若a⊥α,a⊥β,则由平面与平面平行的判定定理得α∥β,故D正确.
故选:D.
若α∥a,α∥b,则a与b相交、平行或异面,故B错误;
若a⊥α,b⊥β,则α与β相交或平行,故C错误;
若a⊥α,a⊥β,则由平面与平面平行的判定定理得α∥β,故D正确.
故选:D.
点评:本小题考查命题真假的判断,是中档题,解题时要注意空间想象能力和思维能力的培养.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
|
| A、充要 |
| B、必要不充分 |
| C、充分不必要 |
| D、既不充分也不必要 |
已知函数y=f(x)的图象如图所示,则下列说法中错误的是( )
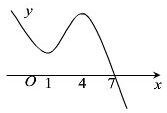

| A、f(x)在区间(-∞,1)上单调递减 |
| B、f(x)在区间(1,4)上单调递增 |
| C、当4<x<7时,f'(x)>0 |
| D、当x=1时,f'(x)=0 |
已知函数y=f(x)是R上的奇函数,且当x≥0时f(x)=x2-2x,则f(x)在(-∞,0]上的解析式是( )
| A、f(x)=x2-2x |
| B、f(x)=-x2-2x |
| C、f(x)=-x2+2x |
| D、f(x)=x2+2x |
下列命题中正确的是( )
| A、函数y=48x-x3有两个极值点 |
| B、函数y=x3-x2+x有两个极值点 |
| C、函数y=x3有且只有1个极值点 |
| D、函数y=ex-x无极值点 |
设集合A={x|x>-1},B={x|x≥1},则“x∈A且x∉B”成立的充要条件是( )
| A、-1<x≤1 | B、x≤1 |
| C、x>-1 | D、-1<x<1 |
下列函数中,值域是(0,+∞)的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=(
|