题目内容
3.已知向量$\overrightarrow a=({1,2}),\overrightarrow b=({2,-3})$,向量$\overrightarrow c$满足$({\overrightarrow c+\overrightarrow a})∥\overrightarrow b,\overrightarrow c⊥({\overrightarrow a+\overrightarrow b})$,则$\overrightarrow c$用基底$\overrightarrow a,\overrightarrow b$的线性表示为$\frac{1}{9}\overrightarrow{b}-\overrightarrow{a}$.分析 由已知可得$\overrightarrow{c}+\overrightarrow{a}=λ\overrightarrow{b}$,$\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})=0$⇒$\overrightarrow{c}=λ\overrightarrow{b}-\overrightarrow{a}$,($λ\overrightarrow{b}-\overrightarrow{a}$)$•(\overrightarrow{a}+\overrightarrow{b}$)=0,⇒λ$\overrightarrow{a}•\overrightarrow{b}$+$λ\overrightarrow{b}$-${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=0⇒λ=$\frac{1}{9}$,即可得$\overrightarrow{c}$=$\frac{1}{9}\overrightarrow{b}-\overrightarrow{a}$.
解答 解:∵向量$\overrightarrow c$满足$({\overrightarrow c+\overrightarrow a})∥\overrightarrow b,\overrightarrow c⊥({\overrightarrow a+\overrightarrow b})$,则$\overrightarrow{c}+\overrightarrow{a}=λ\overrightarrow{b}$,$\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})=0$
⇒$\overrightarrow{c}=λ\overrightarrow{b}-\overrightarrow{a}$,($λ\overrightarrow{b}-\overrightarrow{a}$)$•(\overrightarrow{a}+\overrightarrow{b}$)=0,
⇒λ$\overrightarrow{a}•\overrightarrow{b}$+$λ\overrightarrow{b}$-${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=0,
⇒-4λ+13λ-5+4=0,
⇒λ=$\frac{1}{9}$.
∴$\overrightarrow{c}=λ\overrightarrow{b}-\overrightarrow{a}$=$\frac{1}{9}\overrightarrow{b}-\overrightarrow{a}$,
故答案为:$\frac{1}{9}\overrightarrow{b}-\overrightarrow{a}$.
点评 本题考查了向量的数量积计算、共线得应用,属于中档题.

| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{32}$ | D. | $\frac{7}{8}$ |
| A. | a2>b2 | B. | a3>b3 | C. | $\frac{1}{a}$$<\frac{1}{b}$ | D. | ac>bc |
 已知如图是一个空间几何体的三视图.
已知如图是一个空间几何体的三视图.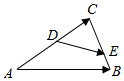 如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.
如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.