题目内容
7.定义在R上的函数y=f(x)关于y轴对称,且在[0,+∞)上是增加的,则下列关系成立的是( )| A. | f(3)<f(-4)<f(-π) | B. | f(-π)<f(-4)<f(3) | C. | f(-4)<f(-π)<f(3) | D. | f(3)<f(-π)<f(-4) |
分析 根据函数奇偶性和单调性之间的关系,即可比较大小.
解答 解:∵函数y=f(x)的图象关于y轴对称,
∴f(x)是偶函数,则f(-4)=f(4),f(-π)=f(π)
∵函数f(x)在区间[0,+∞)上为增函数,
∴f(3)<f(π)<f(4),
即f(3)<f(-π)<f(-4),
故选:D.
点评 本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
17.某几何体的三视图如图所示,则此几何体的体积等于( )
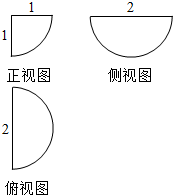

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{8π}{3}$ |
12.如图,在三棱锥P-ABC中,不能证明AP⊥BC的条件是( )
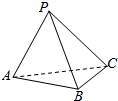

| A. | AP⊥PB,AP⊥PC | B. | AP⊥PB,BC⊥PB | ||
| C. | 平面BPC⊥平面APC,BC⊥PC | D. | AP⊥平面PBC |