题目内容
17.设数列{an}满足a1=2,an+1-an=3•22n-1.(1)求数列{an}的通项公式;
(2)求数列{an}的前n项的和.
分析 (1)利用“累加求和”方法、等比数列的求和公式即可得出.
(2)利用等比数列的求和公式即可得出.
解答 解:(1)由已知,当n≥1时,an+1=(an+1-an)+(an-an-1)+…+(a2-a1)+a1+a1
=3(22n-1+22n-3+…+2)+2=22(n+1)-1.
又a1=2,
∴数列{an}的通项公式为an=22n-1.
(2)数列{an}为等比数列,首项为2,公比为4.
其前n项的和=$\frac{2({4}^{n}-1)}{4-1}$=$\frac{2}{3}({4}^{n}-1)$.
点评 本题考查了“累加求和”方法、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.正项等比数列{an}中,a6=a5+2a4,若存在两项am,an使得$\sqrt{{a_m}{a_n}}$=4a1,则$\frac{1}{m}$+$\frac{2}{n}$的最小值是( )
| A. | $\frac{{3+2\sqrt{2}}}{6}$ | B. | 1 | C. | $\frac{11}{5}$ | D. | $\frac{5}{4}$ |
12.已知直线l过点(0,1),且倾斜角为$\frac{π}{6}$,当此直线与抛物线x2=4y交于A,B时,|AB|=( )
| A. | $\frac{16}{3}$ | B. | 16 | C. | 8 | D. | $\frac{{16\sqrt{3}}}{3}$ |
7.已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上一点,F1,F2为双曲线的左、右焦点,使($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0(O为坐标原点),且|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,则双曲线离心率为( )
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\sqrt{6}$+1 | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
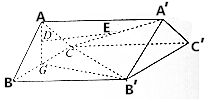 已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.
已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4. 如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.