题目内容
2．
如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′=6，O′C′=2，则原图形OABC的面积为24$\sqrt{2}$．
分析 根据所给的数据做出直观图形的面积，根据直观图的面积：原图的面积=$\frac{\sqrt{2}}{4}$，得到原图形的面积是12÷$\frac{\sqrt{2}}{4}$，得到结果．
解答 解：∵矩形O'A'B'C'是一个平面图形的直观图，其中O'A'=6，O'C'=2，
∴直观图的面积是6×2=12
∵直观图的面积：原图的面积=1：2$\sqrt{2}$，
∴原图形的面积是12÷$\frac{\sqrt{2}}{4}$=24$\sqrt{2}$．
故答案为24$\sqrt{2}$．
点评 本题考查平面图形的直观图，本题解题的关键是知道两个图形的面积之间的关系，遇到类似的题目只要利用公式求出即可．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12．已知2sinxtanx=3，（-π＜x＜0），则x=（ ）
| A． | $-\frac{π}{3}$ | B． | $-\frac{π}{6}$ | C． | $-\frac{5π}{6}$ | D． | $-\frac{2π}{3}$ |
13．已知（-1，y1），（-2，y2），（-4，y3）是抛物线y=-2x2-8x+m上的点，则（ ）
| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y3＜y1＜y2 | D． | y2＜y3＜y1 |
7．各项都是正数的等比数列{an}的公比q≠1，a3，a5，a6成等差数列，则$\frac{{{a_3}+{a_4}}}{{{a_4}+{a_5}}}$=（ ）
| A． | $\frac{{-1+\sqrt{3}}}{2}$ | B． | $\frac{{-1+\sqrt{5}}}{2}$ | C． | $\frac{{1+\sqrt{5}}}{2}$ | D． | $2+\sqrt{5}$ |
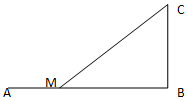如图，设铁路AB长为50，BC⊥AB，且BC=10，为将货物从A运往C，现在AB上距点B为x的点M处修一公路至C，已知单位距离的铁路运费为2，公路运费为4．