题目内容
6.设实数x,y满足x2=4y,则$\sqrt{{{({x-3})}^2}+{{({y-1})}^2}}+y$的最小值是2.分析 抛物线的准线方程为y=-1,$\sqrt{{{({x-3})}^2}+{{({y-1})}^2}}+y$+1-1最小值是(3,1)与焦点(0,1)的距离减去1,可得结论.
解答 解:抛物线的准线方程为y=-1,$\sqrt{{{({x-3})}^2}+{{({y-1})}^2}}+y$+1-1最小值是(3,1)与焦点(0,1)的距离减去1,
即$\sqrt{{{({x-3})}^2}+{{({y-1})}^2}}+y$的最小值是3-1=2,
故答案为2.
点评 本题考查抛物线的方程与性质,考查学生转化问题的能力,属于中档题.

练习册系列答案
相关题目
14.已知命题p:函数$f(x)=\frac{2x+3}{x}$的图象关于(0,3)中心对称;命题q:已知函数g(x)=msinx+ncosx(m,n∈R)满足$g({\frac{π}{6}-x})=g({\frac{π}{6}+x})$,则$n=\sqrt{3}m$; 则下列命题是真命题的为( )
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
15.若?x∈(-1,2),ax+2≠0是假命题的一个充分不必要条件为a∈( )
| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (-∞,-1) | D. | (-∞,-1]∪[2,+∞) |
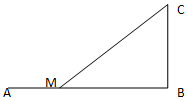 如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.