题目内容
已知函数f(x)=x
(1)求出函数的定义域
(2)判断函数的奇偶性
(3)写出函数的单调区间
(4)做出函数的图象.
| 2 |
| 3 |
(1)求出函数的定义域
(2)判断函数的奇偶性
(3)写出函数的单调区间
(4)做出函数的图象.
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:(1)由函数的解析式求出函数的定义域;
(2)根据函数的奇偶性的定义判断出函数是偶函数;
(3)由幂函数的性质和函数的解析式写出函数的单调区间;
(4)利用函数的性质和幂函数的图象画出f(x)的图象.
(2)根据函数的奇偶性的定义判断出函数是偶函数;
(3)由幂函数的性质和函数的解析式写出函数的单调区间;
(4)利用函数的性质和幂函数的图象画出f(x)的图象.
解答:
解:(1)由题意得,f(x)=x
=
,
由x2≥0得x∈R,所以函数的定义域是R;
(2)由(1)知函数的定义域关于原点对称,
又f(-x)=
=
=f(x),则函数f(x)是偶函数;
(3)函数f(x)的增区间是(0,+∞)和(-∞,0);
(4)由以上的函数的性质和幂函数y=
的图象画出f(x)的图象:
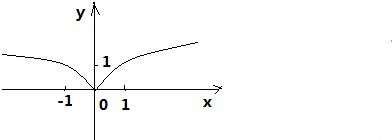 .
.
| 2 |
| 3 |
| 3 | x2 |
由x2≥0得x∈R,所以函数的定义域是R;
(2)由(1)知函数的定义域关于原点对称,
又f(-x)=
| 3 | (-x)2 |
| 3 | x2 |
(3)函数f(x)的增区间是(0,+∞)和(-∞,0);
(4)由以上的函数的性质和幂函数y=
| x |
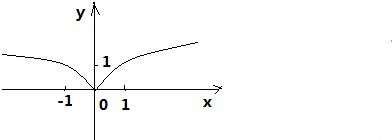 .
.
点评:本题考查幂函数的定义域、奇偶性、单调性,以及幂函数的图象,难度不大,考查数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
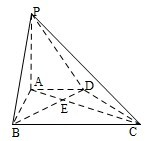 四棱锥P-ABCD中,ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥面ABCD,PA=3,AD=2,AB=2
四棱锥P-ABCD中,ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥面ABCD,PA=3,AD=2,AB=2