题目内容
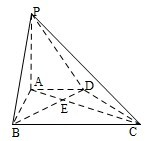四棱锥P-ABCD中，ABCD为直角梯形，AD∥BC，∠ABC=90°，PA⊥面ABCD，PA=3，AD=2，AB=2| 3 |
（1）求证：BD⊥平面PAC；
（2）求二面角P-BD-A大小；
（3）求二面角B-PC-A大小．
考点：二面角的平面角及求法,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）建立空间坐标系，利用向量的数量积，我们可以证明BD⊥AP，BD⊥AC，利用线面垂直的判定定理，我们可证BD⊥平面PAC．
（2）分别求出平面PBD的法向量和平面ABD的法向量，由此利用向量法能求出二面角P-BD-A大小．
（3）分别求出平面PCA的法向量和平面PBC的法向量，由此能求出二面角B-PC-A大小．
（2）分别求出平面PBD的法向量和平面ABD的法向量，由此利用向量法能求出二面角P-BD-A大小．
（3）分别求出平面PCA的法向量和平面PBC的法向量，由此能求出二面角B-PC-A大小．
解答：
（1）证明：如图，以A为原点，AB为x轴，
AD为y轴，AP为z轴，建立坐标系，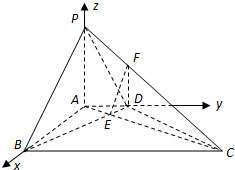
则A（0，0，0），B（2
，0，0），
C（2
，6，0），D（0，2，0），P（0，0，3）
∴
=（0，0，3），
=（-2
，2，0），
=（2
，6，0）
∴
•
=0，
•
=-12+12=0，
∴BD⊥AP，BD⊥AC，又PA∩AC=A
∴BD⊥平面PAC．
（2）解：
=（-2
，0，3），
=（0，-2，3），
设平面PBD的法向量
=（x，y，z），
则
，取x=
，得
=（
，3，2），
又平面ABD的法向量
=（0，0，1），
设二面角P-BD-A的平面角为θ，
则cosθ=|cos＜
，
＞|=|
|=
，
二面角P-BD-A大小为
．
（3）解：
=（0，0，3），
=（2
，6，0），
设平面PCA的法向量
=（a，b，c），
则
，取a=
，得
=（
，-1，0），
=（-2
，0，3），
=（2
，6，-3），
设平面PBC的法向量
=（x1，y1，z1），
则
，取x1=
，得
=（
，0，2），
设二面角B-PC-A的平面角为α，
则cosα=|cos＜
，
＞|=|
|=|
|=
，
∴二面角B-PC-A大小为arccos
．
AD为y轴，AP为z轴，建立坐标系，
则A（0，0，0），B（2
| 3 |
C（2
| 3 |
∴
| AP |
| BD |
| 3 |
| AC |
| 3 |
∴
| AP |
| BD |
| AC |
| BD |
∴BD⊥AP，BD⊥AC，又PA∩AC=A
∴BD⊥平面PAC．
（2）解：
| PB |
| 3 |
| PD |
设平面PBD的法向量
| n |
则
|
| 3 |
| n |
| 3 |
又平面ABD的法向量
| m |
设二面角P-BD-A的平面角为θ，
则cosθ=|cos＜
| m |
| n |
| 2 | ||
|
| 1 |
| 2 |
二面角P-BD-A大小为
| π |
| 3 |
（3）解：
| AP |
| AC |
| 3 |
设平面PCA的法向量
| p |
则
|
| 3 |
| p |
| 3 |
| PB |
| 3 |
| PC |
| 3 |
设平面PBC的法向量
| q |
则
|
| 3 |
| q |
| 3 |
设二面角B-PC-A的平面角为α，
则cosα=|cos＜
| p |
| q |
| ||||
|
|
| 3 | ||
2
|
3
| ||
| 14 |
∴二面角B-PC-A大小为arccos
3
| ||
| 14 |
点评：本题主要考查直线与平面、平面与平面之间的平行、垂直等位置关系，考查线面垂直、二面角的概念、求法等知识，考查空间想象能力和逻辑推理能力，是中档题．
练习册系列答案
相关题目
为了解某校高三毕业班准备报考飞行员学生的体重情况（体重都以整数计），将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第3小组的频数为6；