题目内容
指出下列命题中,p是q的什么条件:
(1)p:{x|x>-2或x<3};q:{x|x2-x-6<0}.
(2)p:-2<m<0,0<n<1;q:关于x的方程x2+mx+n=0有两个小于1的正根.
(1)p:{x|x>-2或x<3};q:{x|x2-x-6<0}.
(2)p:-2<m<0,0<n<1;q:关于x的方程x2+mx+n=0有两个小于1的正根.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义进行判断即可.
解答:
解:(1)p:{x|x>-2或x<3}=R,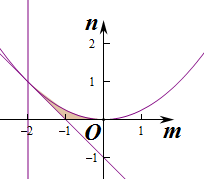
q:{x|x2-x-6<0}={x|-2<x<3}.
则p是q必要不充分条件.
(2)q:关于x的方程x2+mx+n=0有两个小于1的正根.
则设f(x)=x2+mx+n,
则满足
,
即
,则对应的区域为阴影部分,
则p是q的必要不充分条件.
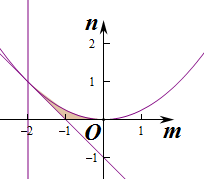
q:{x|x2-x-6<0}={x|-2<x<3}.
则p是q必要不充分条件.
(2)q:关于x的方程x2+mx+n=0有两个小于1的正根.
则设f(x)=x2+mx+n,
则满足
|
即
|
则p是q的必要不充分条件.
点评:本题主要考查充分条件和必要条件的判断,根据条件求出对应命题的等价条件是解决本题的关键.

练习册系列答案
相关题目
在定义域内满足f(x)•f(y)=f(x+y)的函数为( )
| A、f(x)=kx(k≠0) |
| B、f(x)=ax(a>0且a≠1) |
| C、f(x)=logax(a>0且a≠1) |
| D、f(x)=ax2+bx+c(a≠0) |
P是椭圆上的点,F1,F2是它的焦点,∠PF1F2=75°,∠PF2F1=15°,则椭圆的焦距与长轴长之比为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|