题目内容
在△ABC中，∠B=
π，D是BC边上任意一点（D与B、C不重合），且
2+
2-
2=
•
-2
•
，则∠A等于 ．
| 5 |
| 12 |
| AC |
| BC |
| AD |
| BD |
| DC |
| AC |
| CB |
，则∠A等于
考点：平面向量数量积的运算
专题：平面向量及应用
分析：作 AO⊥BC，垂足为 O，以 BC 所在直线为 x 轴，以 OA 所在直线为 y 轴，建立直角坐标系．设 A（0，a），B（b，0），C （c，0），D（d，0）．由
2+
2-
2=
•
-2
•
，可得
2+
2-2
•
=
2+
•
，化为
2=
2+
•
，化简可得b=-c，进而得出．
| AC |
| BC |
| AD |
| BD |
| DC |
| AC |
| CB |
| AC |
| BC |
| AC |
| BC |
| AD |
| BD |
| DC |
| AB |
| AD |
| BD |
| DC |
解答：
解：作 AO⊥BC，垂足为 O，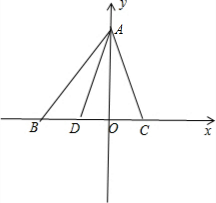
以 BC 所在直线为 x 轴，以 OA 所在直线为 y 轴，建立直角坐标系．
设 A（0，a），B（b，0），C （c，0），D（d，0）．
∵
2+
2-
2=
•
-2
•
，
∴
2+
2-2
•
=
2+
•
，
∴
2=
2+
•
，
∴b2+a2=d2+a2+（d-b）（c-d），
即（b-d）（b+d）=（d-b）（d-c），
又b-d≠0，
∴b+d=d-c，
∴b=-c，
∴点B（b，0）和C（c，0）关于原点对称，
∴△ABC为等腰三角形．
∴AB=AC，∵∠B=
，
∴∠A=π-
π×2=
．
故答案为：
．
以 BC 所在直线为 x 轴，以 OA 所在直线为 y 轴，建立直角坐标系．
设 A（0，a），B（b，0），C （c，0），D（d，0）．
∵
| AC |
| BC |
| AD |
| BD |
| DC |
| AC |
| CB |
∴
| AC |
| BC |
| AC |
| BC |
| AD |
| BD |
| DC |
∴
| AB |
| AD |
| BD |
| DC |
∴b2+a2=d2+a2+（d-b）（c-d），
即（b-d）（b+d）=（d-b）（d-c），
又b-d≠0，
∴b+d=d-c，
∴b=-c，
∴点B（b，0）和C（c，0）关于原点对称，
∴△ABC为等腰三角形．
∴AB=AC，∵∠B=
| 5π |
| 12 |
∴∠A=π-
| 5 |
| 12 |
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：本题考查了向量的数量积运算性质、余弦定理、等腰三角形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在四棱柱中，底面是等腰梯形，AB∥CD，AB=2，BC=CD=1，顶点D1在底面ABCD内的射影恰好为C，
求证：AD1⊥BC，若DD1与AB所成的角为60°，求面ABC1D1和面ABCD的余弦函数值．
求证：AD1⊥BC，若DD1与AB所成的角为60°，求面ABC1D1和面ABCD的余弦函数值．
为了解某校高三毕业班准备报考飞行员学生的体重情况（体重都以整数计），将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第3小组的频数为6；P是椭圆上的点，F1，F2是它的焦点，∠PF1F2=75°，∠PF2F1=15°，则椭圆的焦距与长轴长之比为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某四棱锥的三视图如图所示，该四棱锥的表面积为（ ）
| A、17 | ||
| B、22 | ||
C、14+2
| ||
D、22+2
|