题目内容
在△ABC中，|
|=|
|=3，∠ABC=60°，AD是边BC上的高，则
•
的值等于（ ）
| AB |
| BC |
| AD |
| AC |
A、-
| ||
B、
| ||
C、
| ||
| D、9 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据已知条件可以分别以BC，DA所在直线为x，y轴建立平面直角坐标系，而根据已知的边长及角的值可求出向量
，
的坐标，根据数量积的坐标运算即可求出
•
．
| AD |
| AC |
| AD |
| AC |
解答：
解：分别以BC，AD所在直线为x轴，y轴建立如图所示平面直角坐标系；
根据已知条件可求以下几点坐标：
A（0，
），D（0，0），C（
，0）；
∴
=(0，-
)，
=(
，-
)；
∴
•
=
．
故选C．
根据已知条件可求以下几点坐标：A（0，
3
| ||
| 2 |
| 3 |
| 2 |
∴
| AD |
3
| ||
| 2 |
| AC |
| 3 |
| 2 |
3
| ||
| 2 |
∴
| AD |
| AC |
| 27 |
| 4 |
故选C．
点评：考查通过建立平面直角坐标系，通过坐标解决向量问题的方法，由点的坐标求向量的坐标，以及向量数量积的坐标运算．
练习册系列答案
阅读快车系列答案
相关题目
集合A={y|y=
}，B={y|y=x2+2}，则A∩B表示的集合为（ ）
| x+1 |
| A、{x|x≥1} |
| B、{x|x≥2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x＜2} |
若直线（m+2）x+3y+3=0与直线x+（2m-1）y+m=0平行，则实数m=（ ）
A、-
| ||
| B、1 | ||
| C、1或2 | ||
D、-
|
一块电路板的AB线段之间有60个串联的焊接点，知道电路不通的原因是焊口脱落造成的．要想用二分法的思想检测出哪处焊口脱落．至少需要检测（ ）
| A、4次 | B、6次 | C、8次 | D、30次 |
平面向量
，
的夹角为60°，
=（2，0），|
|=1，则|
+2
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
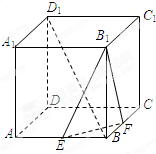如图，在正方体ABCD-A1B1C1D1中，棱AB=1，点E、F分别是AB、BC的中点．