题目内容
20. 如图,等腰直角△ABC中,AB=AC=1,在边AB、AC上分别取D、E两点,沿线段DE折叠,顶点A恰好落在边BC上,则AD长度的最小值为$\sqrt{2}$-1..
如图,等腰直角△ABC中,AB=AC=1,在边AB、AC上分别取D、E两点,沿线段DE折叠,顶点A恰好落在边BC上,则AD长度的最小值为$\sqrt{2}$-1..
分析 如图,连接AA′,设∠BDA′=θ∈$(0,\frac{3π}{4})$.可设AD=DP=x,AB=1,则BD=1-x.在△BDA′中,由正弦定理有:$\frac{BD}{sin∠B{A}^{′}D}$=$\frac{1-x}{sin(\frac{3π}{4}-θ)}$=$\frac{x}{sinB}$=$\sqrt{2}$x.可得:x=$\frac{1}{\sqrt{2}sin(\frac{3π}{4}-θ)+1}$.即可得出.
解答 解:如图,连接AA′,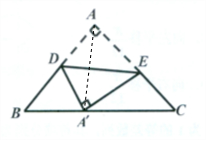 设∠BDA′=θ∈$(0,\frac{3π}{4})$.
设∠BDA′=θ∈$(0,\frac{3π}{4})$.
由AD=DA′,
可设AD=DP=x,AB=1,则BD=1-x
在△BDA′中,由正弦定理有:$\frac{BD}{sin∠B{A}^{′}D}$=$\frac{1-x}{sin(\frac{3π}{4}-θ)}$=
$\frac{x}{sinB}$=$\frac{x}{sin\frac{π}{4}}$=$\sqrt{2}$x.
可得:x=$\frac{1}{\sqrt{2}sin(\frac{3π}{4}-θ)+1}$.
∴当θ=$\frac{π}{4}$时,x取得最小值,x=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 本题考查了正弦定理、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.若复数z满足z(-1+2i)=|1+3i|2,(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.在△ABC中,AB=$\sqrt{3}$,A=45°,C=60°,则BC=( )
| A. | 3-$\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3+$\sqrt{3}$ |
8.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的一条渐近线与直线x-2y+4=0垂直,则b=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
12.已知两点F1(-1,0)、F2(1,0),若|F1F2|是|PF1|与|PF2|的等差中项,则动点P的轨迹方程是( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 |