题目内容
对于任意实数a,b,不等式max{|a+b|,|a-b|,|2006-b|}≥C恒成立,则常数C的最大值是 .(注:max{x,y,z}表示x,y,z中的最大者.)
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:利用题中的定义设出三者的最大值,列出不等式,相加,利用绝对值的性质求出M的最小值,求出c的范围.
解答:
解:设M=max{|a+b|,|a-b|,|2006-b|},
则M≥|a+b|;M≥|b-a|;2M≥|4012-2b|,
相加得:
4M≥|a+b|+|b-a|+|4012-2b|≥|a+b+b-a+4012-2b|=4012,
即M≥1003,
当a+b,b-a,4012-2b同号时取等号.
即当a=0,b=1003时,M=1003,等号成立,即M的最小值为1003,
也即C的最大值为1003.
故答案为:1003.
则M≥|a+b|;M≥|b-a|;2M≥|4012-2b|,
相加得:
4M≥|a+b|+|b-a|+|4012-2b|≥|a+b+b-a+4012-2b|=4012,
即M≥1003,
当a+b,b-a,4012-2b同号时取等号.
即当a=0,b=1003时,M=1003,等号成立,即M的最小值为1003,
也即C的最大值为1003.
故答案为:1003.
点评:本题考查理解题中的新定义;绝对值不等式的性质;不等式恒成立求参数范围转化成求函数的最值;解分式不等式等,是中档题.

练习册系列答案
相关题目
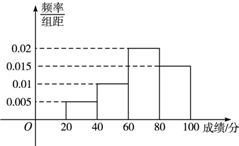 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )| A、63 | B、65 | C、68 | D、70 |
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )| A、a=b=c |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |