题目内容
11.设函数$f(x)=-\frac{1}{3}{x^3}+2a{x^2}-3{a^2}x+\frac{1}{3}a$(0<a<1)(1)若函数f(x)的单调区间;
(2)若当x∈[a,2]时,恒有f(x)≤0成立,试确定a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)通过讨论a的范围,得到关于f(x)的单调区间,求出f(x)在[a,2]的最大值,得到关于a的不等式,解出即可.
解答 解:(1)f'(x)=-x2+4ax-3a2.令f'(x)=-x2+4ax-3a2=0,得x=a或x=3a,
令f′(x)>0,解得:a<x<3a,令f′(x)<0,解得:x>3a或x<a,
故f(x)在(-∞,a)递减,在(a,3a)递增,在(3a,+∞)递减;
(2)由(1)得:f(x)在(a,3a)递增,在(3a,+∞)递减;
3a≤2即0<a<$\frac{2}{3}$时,f(x)在[a,3a)递增,在(3a,2]递减,
f(x)max=f(3a)=$\frac{1}{3}$a≤0,不合题意;
3a≥2即$\frac{2}{3}$≤a<1时,f(x)在[a,2]递增,
f(x)max=f(2)=-6a2+$\frac{25}{3}$a-$\frac{8}{3}$≤0,
解得:a≥$\frac{8}{9}$,
综上:a∈[$\frac{8}{9}$,1).
点评 本题考查了函数的单调性、最值问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
2.a,b,c是△ABC中角A,B,C的对边,则直线sinAx+ay+c=0与sinBx+by=0的位置关系是( )
| A. | 相交 | B. | 重合 | C. | 垂直 | D. | 平行 |
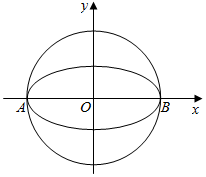 如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,其左顶点A在圆O:x2+y2=16上.