题目内容
6.已知命题p:关于x的方程x2-ax+1=0有实根;命题q:对任意x∈[-1,1],不等式a2-3a-x+1≤0恒成立,若“p∧q”是假命题,“?q”也是假命题,求实数a的取值范围.分析 结合三个二次关系分别求得命题p,q为真命题时的a的取值范围,由“p∧q”是假命题,“?q”也是假命题确定p,q的真假,从而得到a的不等式,确定其取值范围.
解答 解:若p真,则△=a2-4×1≥0,∴a≤-2或a≥2.
若q真,则由对任意 x∈[-1,1],不等式 x-1≥a2-3a恒成立,
∴( x-1)min≥a2-3a 即a2-3a≤-2 解得1≤a≤2,即q为真命题时,a 的取值范围是[1,2].
∵“p∧q”是假命题,“?q”也是假命题,则p是假命题,q是真命题∴$\left\{\begin{array}{l}-2<a<2\\ 1≤a≤2\end{array}\right.$,
∴1≤a<2,∴实数a的取值范围为[1,2).
点评 本题考查了复合命题的真假判断,考查了一元二次不等式的解法,是中档题.

练习册系列答案
相关题目
14.表面积为20π的球面上有四点S、A、B、C,且△ABC是边长为2$\sqrt{3}$的等边三角形,若平面SAB⊥平面ABC,则三棱锥S-ABC体积的最大值是( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
1.已知等比数列{an}中,a2+a5=18,a3•a4=32,若an=128,则n=( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )



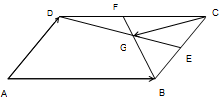 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量